题目内容

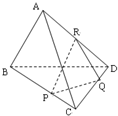（理科）已知如图，四面体ABCD中，P，Q，R分别在棱BC，CD，DA上，且BP=2PC，CQ=2QD，DR=RA，则A，B两点到平面PQR的距离之比为（　　）
A、1：4B、1：3
C、1：2D、1：1
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：分别设A，D，C，B到平面PQR的距离为d1，d2，d3，d4，由已知条件推导出d1=d2，d3=2d2，d4=2d3，由此能求出A，B两点到平面PQR的距离之比．
解答： 解：分别设A，D，C，B到平面PQR的距离为d1，d2，d3，d4，
∵AR=RD，∴d1=d2，
∵CQ=2QD，∴d3=2d2，
∵BP=2PC，∴d4=2d3，
∴d4=4d1，
∴A，B两点到平面PQR的距离之比为1：4．
故选：A．
点评：本题考查两点到平面的距离之比的求法，是中档题，解题时要认真审题，注意合理地化空间问题为平面问题．
练习册系列答案
相关题目
在△ABC中，三边长分别为a，b，c，且A=30°，B=45°，a=1，则b的值是（　　）
A、
1
2
B、
2
2
C、
2
D、
6
2
将一颗骰子连续抛掷三次，已知它落地时向上的点数恰好依次成等差数列，那么这三次抛掷向上的点数之和为12的概率为（　　）
A、
5
18
B、
1
9
C、
3
18
D、
1
72
如图，矩形ABCD和矩形ABEF中，矩形ABEF可沿AB任意翻折，AF=AD，M、N分别在AE、DB上运动，当F、A、D不共线，M、N不与A、D重合，且AM=DN时，有（　　）
A、MN∥平面FAD
B、MN与平面FAD相交
C、MN⊥平面FAD
D、MN与平面FAD可能平行，也可能相交
若
x≤2
y≤2
x+y≥3
，则目标函数z=
x+2y
x
的取值范围是（　　）
A、[2，5]
B、[1，5]
C、[
1
2
，2]
D、[2，6]
下列叙述中，正确的个数是（　　）
①命题p：“?x∈R，x2-2≥0”的否定形式为￢p：“?x∈R，x2-2＜0”；
②O是△ABC所在平面上一点，若
OA
•
OB
=
OB
•
OC
=
OC
•
OA
，则O是△ABC的垂心；
③“M＞N”是“（
2
3
）M＞（
2
3
）N”的充分不必要条件；
④命题“若x2-3x-4=0，则x=4”的逆否命题为“若x≠4，则x2-3x-4≠0”；
⑤已知
a
=（2，-1），
b
=（m，m-1），则
a
和
b
的夹角为锐角充要条件为：m＞-1．
A、1B、2C、3D、4
已知函数f（x）=ax3+bx2在点（3，f（3））处的切线方程为12x+2y-27=0．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若方程f(x)=-
1
2
x2+m有三个不同的解，求实数m的取值范围；
（Ⅲ）若不等式f(x)-
3
2
x2+(k+1)x≥0(k∈R)对于x∈（-∞，0）恒成立，求实数k的取值范围．
已知向量
a
=（2，1），
b
=（x，y）
（Ⅰ）若x∈{-1，0，1}，y∈{-2，-1，2}，求向量
a
⊥
b
的概率；
（Ⅱ）若用计算机产生的随机二元数组（x，y）构成区域Ω：
-1＜x＜1
-2＜y＜2
，求二元数组（x，y）满足x2+y2≥1的概率．
已知△ABC中，B，C所对的边分别为a，b，c，cosA=
3
5
，b=5
3
，B=
π
3
，则a=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网