题目内容
已知f（x）是定义在R上的偶函数，对任意x∈R，都有f（x+4）=f（x）+2f（2），且f（-1）=2，则f（2013）等于 ．
考点：函数奇偶性的判断,抽象函数及其应用
专题：函数的性质及应用
分析：根据条件求出f（2）的值，根据函数的周期性即可得到结论．
解答：
解：∵f（x）是定义在R上的偶函数，对任意x∈R，都有f（x+4）=f（x）+2f（2），
∴当x=-2时，有f（2）=f（2）+2f（2），即f（2）=0，
∴f（x+4）=f（x），即函数的周期是4，
∴f（2013）=f（503×4+1）=f（1），
∵f（-1）=2，
∴f（-1）=f（1）=2，
即f（2013）=2，
故答案为：2
∴当x=-2时，有f（2）=f（2）+2f（2），即f（2）=0，
∴f（x+4）=f（x），即函数的周期是4，
∴f（2013）=f（503×4+1）=f（1），
∵f（-1）=2，
∴f（-1）=f（1）=2，
即f（2013）=2，
故答案为：2
点评：本题主要考查函数值的计算，利用函数的奇偶性得到函数的周期性是解决本题的关键．
练习册系列答案
相关题目
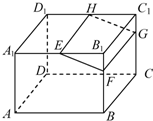如图，在长方体ABCD-A1B1C1D1中，E，H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G．设AB=2AA1=2a，EF=a，B1E=2B1F．在长方体ABCD-A1B1C1D1内随机选取一点，则该点取自于几何体A1ABFE-D1DCGH内的概率为
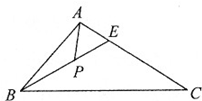在△ABC中，E为AC上一点，且已知复数z=
，则|z|=（ ）
| ||
(1-
|
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|