题目内容
17. 某市的出租车收费办法如下:
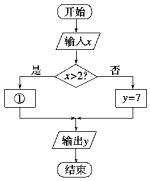
某市的出租车收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
| A. | y=7+2.5x | B. | y=8+2.5x | C. | y=2+2.5x | D. | y=3+2.5x |
分析 由已知中可知当满足条件x>2时,即里程超过2公里,应按超过2公里的里程每公里收2.5元,另每车次超过2公里收燃油附加费1元收费,由收费方式易得函数的解析式.
解答 解:当满足条件x>2时,
即里程超过2公里,
应按超过2公里的里程每公里收2.5元,
另每车次超过2公里收燃油附加费1元收费,
∴y=2.5(x-2)+7+1=8+2.5(x-2)=3+2.5x
故选D.
点评 程序填空是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.

练习册系列答案
相关题目
8.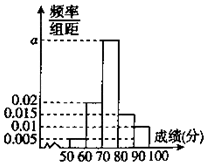 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
2.曲线y=$\frac{x}{x-2}$在点(1,-1)处的切线方程为( )
| A. | y=x-3 | B. | y=-2x+1 | C. | y=2x-4 | D. | y=-2x-3 |
6.集合A={x|-2<x<3},B={x∈Z|x2-5x<0},则A∩B=( )
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {2,3,4} |
7.下列所示的四幅图中,是函数图象的是( )
| A. |  | B. |  | C. |  | D. |  |
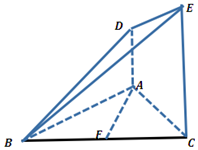 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,