题目内容
9.y=log0.5[cos($\frac{x}{3}$+$\frac{π}{4}$)]的单调递增区间为[6kπ-$\frac{3π}{4}$,6kπ+$\frac{3π}{4}$)(k∈Z).分析 令t=cos($\frac{x}{3}$+$\frac{π}{4}$),则y=log0.5t,本题即求当t>0时,函数t的减区间,再利用余弦函数的性质,得出结论.
解答 解:令t=cos($\frac{x}{3}$+$\frac{π}{4}$),则y=log0.5t,本题即求当t>0时,函数t的减区间,
令2kπ≤$\frac{x}{3}$+$\frac{π}{4}$<2kπ+$\frac{π}{2}$,求得6kπ-$\frac{3π}{4}$≤x<6kπ+$\frac{3π}{4}$,故函数y的增区间为[6kπ-$\frac{3π}{4}$,6kπ+$\frac{3π}{4}$),(k∈Z),
故答案为:[6kπ-$\frac{3π}{4}$,6kπ+$\frac{3π}{4}$)(k∈Z).
点评 本题主要考查复合函数的单调性,余弦函数、对数函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离为$\sqrt{2}$的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 某市的出租车收费办法如下:
某市的出租车收费办法如下:
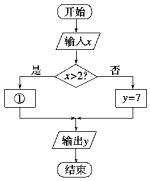
不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
 某市的出租车收费办法如下:
某市的出租车收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
| A. | y=7+2.5x | B. | y=8+2.5x | C. | y=2+2.5x | D. | y=3+2.5x |