题目内容

7．下列所示的四幅图中，是函数图象的是（　　）
A．B．C．D．

分析 利用函数的定义，即可判断．

解答 解：在函数定义中，取集合A中的任何一个元素x，都能在集合B中找个唯一一个元素y与之对应，选项D具有这样的特点，而其他选项没有．
故选：D．

点评 本题考查函数的定义，函数的对应关系的特点是：一对一或多对一．

练习册系列答案
相关题目
17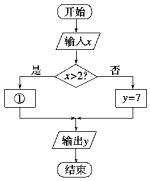．某市的出租车收费办法如下：
不超过2公里收7元（即起步价7元），超过2公里的里程每公里加收2.5元，另外每车次超过2公里收燃油附加费1元（不考虑其他因素）．相应收费系统的程序框图如图所示，则①处应填（　　）
A．y=7+2.5xB．y=8+2.5xC．y=2+2.5xD．y=3+2.5x
18．已知集合A={x|x＜-1或x≥1}，B={x|2a＜x≤a+1，a＜1}，A∪B=A，求实数a的取值范围．
15．如果直线 x+2ay-1=0与直线（3a-1）x-ay-1=0平行，则系数a的值为（　　）
A．0或6B．0或$\frac{1}{6}$C．6或 $\frac{1}{6}$D．$\frac{1}{6}$
2．已知向量 $\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（3，m）．若 （$\overrightarrow{a}$+2$\overrightarrow{b}$）∥（3$\overrightarrow{b}$-$\overrightarrow{a}$），则实数 m 的值是$\frac{3}{2}$．
12．已知函数F（x）=lnx（x＞1）的图象与函数G（x）的图象关于直线y=x对称，若函数f（x）=（k-1）x-G（-x）无零点，则实数k的取值范围是（　　）
A．（1-e，1）B．（1-e，∞）C．（1-e，1]D．（-∞，1-e）∪[1，+∞）
19．《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一，书中有这样一道题：把120个面包分成5份，使每份的面包数成等差数列，且较多的三份之和恰好是较少的两份之和的7倍，则最多的那份有面包（　　）
A．43个B．45个C．46个D．48个
16．已知数列{an}的前n项和${S_n}={n^2}+{a_n}-1$，且a1，a4是等比数列{bn}的前两项，记bn与bn+1之间包含的数列{an}的项数为cn，如b1与b2之间包含{an}中的项为a2，a3，则c1=2．
（1）求数列{an}和{bn}的通项公式；
（2）求数列{ancn}的前n项和．
17．已知向量$\overrightarrow{a}$=（2，m），$\overrightarrow{b}$=（1，-2）若$\overrightarrow{a}$•（$\overrightarrow{a}$-2$\overrightarrow{b}$）=$\overrightarrow{b}$2+m2，则实数m等于（　　）
A．$\frac{1}{2}$B．$\frac{5}{2}$C．$\frac{\sqrt{5}}{4}$D．$\frac{5}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网