题目内容
6．集合A={x|-2＜x＜3}，B={x∈Z|x2-5x＜0}，则A∩B=（ ）| A． | {1，2} | B． | {2，3} | C． | {1，2，3} | D． | {2，3，4} |
分析 由一元二次不等式的解法求出集合B，由交集的运算求出A∩B．
解答 解：∵集合B={x∈Z|x2-5x＜0}={x∈Z|0＜x＜5}={1，2，3，4}，
且集合A={x|-2＜x＜3}，
∴A∩B={1，2}，
故选A．
点评 本题考查了交集及其运算，以及一元二次不等式的解法，属于基础题．
练习册系列答案
相关题目
16．已知函数f（x）=e|x|+x2，且f（3a-2）＞f（a-1），则实数a的取值范围为（ ）
| A． | （0，$\frac{1}{2}$）∪（$\frac{3}{4}$，+∞） | B． | （-∞，$\frac{1}{2}$）∪（$\frac{3}{4}$，+∞） | C． | （$\frac{1}{2}$，+∞） | D． | （-∞，$\frac{1}{2}$） |
17．
某市的出租车收费办法如下：
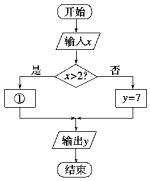
不超过2公里收7元（即起步价7元），超过2公里的里程每公里加收2.5元，另外每车次超过2公里收燃油附加费1元（不考虑其他因素）．相应收费系统的程序框图如图所示，则①处应填（ ）
某市的出租车收费办法如下：不超过2公里收7元（即起步价7元），超过2公里的里程每公里加收2.5元，另外每车次超过2公里收燃油附加费1元（不考虑其他因素）．相应收费系统的程序框图如图所示，则①处应填（ ）
| A． | y=7+2.5x | B． | y=8+2.5x | C． | y=2+2.5x | D． | y=3+2.5x |
15．如果直线 x+2ay-1=0与直线（3a-1）x-ay-1=0平行，则系数a的值为（ ）
| A． | 0或6 | B． | 0或$\frac{1}{6}$ | C． | 6或 $\frac{1}{6}$ | D． | $\frac{1}{6}$ |