题目内容
15.判断下列函数的奇偶性:(1)y=sin(x+$\frac{π}{2}$)
(2)y=cos(α+π)
分析 利用诱导公式化简函数,再利用偶函数的定义进行判断.
解答 解:(1)f(x)=cosx,则f(-x)=f(x),函数是偶函数;
(2)g(α)=-cosα,则g(-α)=g(α),函数是偶函数.
点评 本题考查诱导公式的运用,考查函数的奇偶性,比较基础.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
6.已知i是虚数单位,则复数$\frac{2i}{1+i}$的虚部为( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
3.在2015年春节期间,某商场对销售的某商品一天的投放量x及其销量y进行调查,发现投放量x和销售量y之间的一组数据如表所示:
通过分析,发现销售量y对投放量x具有线性相关关系.
(Ⅰ)求销售量y对投放量x的回归直线方程;
(Ⅱ)欲使销售量为8,则投放量应定为多少.(保留小数点后一位数)
| 投放量x | 6 | 8 | 10 | 12 |
| 销售量y | 2 | 3 | 5 | 6 |
(Ⅰ)求销售量y对投放量x的回归直线方程;
(Ⅱ)欲使销售量为8,则投放量应定为多少.(保留小数点后一位数)
10.将函数y=sinx的图象的横坐标扩大3倍,再将图象向右平移3个单位,所得解析为( )
| A. | y=sin(3x+1) | B. | y=sin($\frac{1}{3}$x-1) | C. | y=sin(3x+3) | D. | y=sin($\frac{1}{3}$x-3) |
7.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离为$\sqrt{2}$的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知函数f(x)=e|x|+x2,且f(3a-2)>f(a-1),则实数a的取值范围为( )
| A. | (0,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | (-∞,$\frac{1}{2}$) |
17.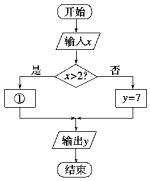 某市的出租车收费办法如下:
某市的出租车收费办法如下:
不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
 某市的出租车收费办法如下:
某市的出租车收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
| A. | y=7+2.5x | B. | y=8+2.5x | C. | y=2+2.5x | D. | y=3+2.5x |