题目内容
2.曲线y=$\frac{x}{x-2}$在点(1,-1)处的切线方程为( )| A. | y=x-3 | B. | y=-2x+1 | C. | y=2x-4 | D. | y=-2x-3 |
分析 先求得y在点(1,-1)处的导数为-2,利用点斜式求得函数y在点(1,-1)处的切线方程.
解答 解:对于函数y=$\frac{x}{x-2}$,∵y′=$\frac{-2}{{(x-2)}^{2}}$,∴y在点(1,-1)处的导数为-2,
故y=$\frac{x}{x-2}$在点(1,-1)处的切线斜率为-2,故y=$\frac{x}{x-2}$在点(1,-1)处的切线方程为y+1=-2(x-1),
即y=-2x+1,
故选:B.
点评 本题主要考查函数在某一点的导数的意义,求曲线在某一点切线的方程,属于中档题.

练习册系列答案
相关题目
10.计算$\frac{{a}^{2}}{\sqrt{a}•\root{3}{{a}^{2}}}$的结果为( )
| A. | a${\;}^{\frac{3}{2}}$ | B. | a${\;}^{\frac{1}{6}}$ | C. | a${\;}^{\frac{5}{6}}$ | D. | a${\;}^{\frac{6}{5}}$ |
17. 某市的出租车收费办法如下:
某市的出租车收费办法如下:
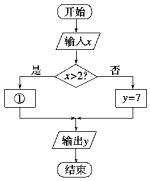
不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
 某市的出租车收费办法如下:
某市的出租车收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里加收2.5元,另外每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
| A. | y=7+2.5x | B. | y=8+2.5x | C. | y=2+2.5x | D. | y=3+2.5x |
7.在空间直角坐标系中,点A(-4,-1,-9)与点B(-10,1,-6)的距离是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
12.已知函数F(x)=lnx(x>1)的图象与函数G(x)的图象关于直线y=x对称,若函数f(x)=(k-1)x-G(-x)无零点,则实数k的取值范围是( )
| A. | (1-e,1) | B. | (1-e,∞) | C. | (1-e,1] | D. | (-∞,1-e)∪[1,+∞) |
 如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.