题目内容
设直线x+y=1与椭圆
+
=1(a>b>0)相交于A,B两点.
(1)若a=
,求b的范围;
(2)若OA⊥OB,且椭圆上存在一点P其横坐标为
,求点P的纵坐标;
(3)若OA⊥OB,且S△OAB=
,求椭圆方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若a=
| ||
| 3 |
(2)若OA⊥OB,且椭圆上存在一点P其横坐标为
| ||
| 2 |
(3)若OA⊥OB,且S△OAB=
| 5 |
| 8 |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)将直线x+y=1代入椭圆方程,消去y,得到x的方程,运用判别式大于0,解出即可;
(2)将直线x+y=1代入椭圆方程,消去y,得到x的方程,运用韦达定理,以及两直线垂直的条件,化简整理,即可得到所求值;
(3)设直线x+y=1与坐标轴交于C、D,求出CD,再由面积,求得AB,再由弦长公式,求得a,b的方程,再由(2)的结论,即可得到椭圆方程.
(2)将直线x+y=1代入椭圆方程,消去y,得到x的方程,运用韦达定理,以及两直线垂直的条件,化简整理,即可得到所求值;
(3)设直线x+y=1与坐标轴交于C、D,求出CD,再由面积,求得AB,再由弦长公式,求得a,b的方程,再由(2)的结论,即可得到椭圆方程.
解答:
解:(1)将直线x+y=1代入椭圆方程,
消去y,得(b2+a2)x2-2a2x+a2-a2b2=0,
x1+x2=
,x1x2=
,
因为直线与椭圆交于两点,故△=4a4-4(b2+a2)(a2-a2b2)>0,
代入a=
,解得b>
,且a>b,
所以b的范围为(
,
);
(2)将直线x+y=1代入椭圆方程,
可得:x1+x2=
,x1x2=
,
由OA⊥OB可得x1x2+y1y2=0,解得a2+b2=2a2b2
即
+
=1,代x0=
到椭圆方程得
+
=1,
即
=
,
所以点P的纵坐标为±
.
(3)设直线x+y=1与坐标轴交于C、D,则CD=
,S△COD=
,
又△AOB,△COD两个三角形等高,故
=
=
,
所以AB=
=
|x1-x2|,求得a2b2=
所以a2=4,b2=
,
所以椭圆方程为
+
=1.
消去y,得(b2+a2)x2-2a2x+a2-a2b2=0,
x1+x2=
| 2a2 |
| a2+b2 |
| a2-a2b2 |
| a2+b2 |
因为直线与椭圆交于两点,故△=4a4-4(b2+a2)(a2-a2b2)>0,
代入a=
| ||
| 3 |
| ||
| 3 |
所以b的范围为(
| ||
| 3 |
| ||
| 3 |
(2)将直线x+y=1代入椭圆方程,
可得:x1+x2=
| 2a2 |
| a2+b2 |
| a2-a2b2 |
| a2+b2 |
由OA⊥OB可得x1x2+y1y2=0,解得a2+b2=2a2b2
即
| 1 |
| 2a2 |
| 1 |
| 2b2 |
| ||
| 2 |
| 1 |
| 2a2 |
| ||
| b2 |
即
| y | 2 0 |
| 1 |
| 2 |
所以点P的纵坐标为±
| ||
| 2 |
(3)设直线x+y=1与坐标轴交于C、D,则CD=
| 2 |
| 1 |
| 2 |
又△AOB,△COD两个三角形等高,故
| AB |
| CD |
| S△AOB |
| S△COD |
| 5 |
| 4 |
所以AB=
5
| ||
| 4 |
| 2 |
| 16 |
| 7 |
所以a2=4,b2=
| 4 |
| 7 |
所以椭圆方程为
| x2 |
| 4 |
| 7y2 |
| 4 |
点评:本题考查椭圆方程及运用,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理和判别式大于0,以及弦长公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
椭圆3x2+ky2=1的一个焦点的坐标为(0,1),则其离心率为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
下列不等式一定成立的是( )
A、lg(x2+
| ||||||
B、sinx+
| ||||||
C、
| ||||||
D、
|
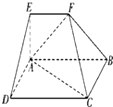 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为 为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: