题目内容
二面角α-l-β的大小为45°,线段AB?α,B∈l,AB与l所成角为45°,则AB与β所成角为 .
考点:直线与平面所成的角
专题:计算题,作图题,空间位置关系与距离
分析:作出图象,构造出题意中的角,通过直角三角形计算即可.
解答:
 解:如右图:
解:如右图:
在平面α内过点A作AC⊥l,垂足为C,在平面β内过点C作EC⊥l,在平面ACE内作AD⊥CE,垂足为D,
则由题意可得,
∠ABC=∠ACD=45°,
则在Rt△ACD中,AC=
AD,
在Rt△ABC中,AB=
AC=2AD,
在Rt△ABD中,sin∠ABD=
=
,
则∠ABD=30°,
易知∠ABD是AB与β所成角,
即AB与β所成角为30°.
故答案为:30°.
 解:如右图:
解:如右图:在平面α内过点A作AC⊥l,垂足为C,在平面β内过点C作EC⊥l,在平面ACE内作AD⊥CE,垂足为D,
则由题意可得,
∠ABC=∠ACD=45°,
则在Rt△ACD中,AC=
| 2 |
在Rt△ABC中,AB=
| 2 |
在Rt△ABD中,sin∠ABD=
| AD |
| AB |
| 1 |
| 2 |
则∠ABD=30°,
易知∠ABD是AB与β所成角,
即AB与β所成角为30°.
故答案为:30°.
点评:本题主要考查了学生的作图能力,同时考查了三角函数的定义,属于中档题.

练习册系列答案
相关题目
下列命题错误的是( )
| A、命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” |
| B、若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 |
| C、△ABC中,sinA>sinB是A>B的充要条件 |
| D、若p∧q为假命题,则p、q均为假命题 |
 如图,四边形ABCD中,AB=AD=CD=1,BD=
如图,四边形ABCD中,AB=AD=CD=1,BD=| 2 |
| A、A′C⊥BD | ||
| B、∠BA′C=90° | ||
| C、CA′与平面A′BD所成的角为30° | ||
D、四面体A′-BCD的体积为
|
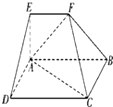 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为