题目内容
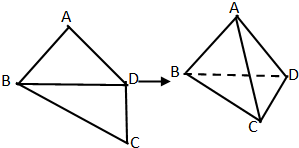 如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=
如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AD⊥平面ABC |
考点:平面与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:对四个结论分别加以判断,即可得出结论.
解答:
解:对于A,∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BD⊥CD,
∴CD⊥平面ABD,∴平面ACD⊥平面ABD,即A正确;
对于B,∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB?平面ABD,AB⊥BD,
∴AB⊥平面BCD,又CD?平面BCD,∴AB⊥CD,即B正确;
对于C,∵AB⊥AD,AB⊥CD,AD∩CD=D,∴AB⊥平面ACD,∴平面ABC⊥平面ACD,即C正确;
对于D,若AD⊥平面ABC,则AD⊥AC,与CD⊥AD矛盾,
故选:D.
∴CD⊥平面ABD,∴平面ACD⊥平面ABD,即A正确;
对于B,∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB?平面ABD,AB⊥BD,
∴AB⊥平面BCD,又CD?平面BCD,∴AB⊥CD,即B正确;
对于C,∵AB⊥AD,AB⊥CD,AD∩CD=D,∴AB⊥平面ACD,∴平面ABC⊥平面ACD,即C正确;
对于D,若AD⊥平面ABC,则AD⊥AC,与CD⊥AD矛盾,
故选:D.
点评:本题考查平面与平面垂直的判定,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
椭圆3x2+ky2=1的一个焦点的坐标为(0,1),则其离心率为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,四边形ABCD中,AB=AD=CD=1,BD=
如图,四边形ABCD中,AB=AD=CD=1,BD=| 2 |
| A、A′C⊥BD | ||
| B、∠BA′C=90° | ||
| C、CA′与平面A′BD所成的角为30° | ||
D、四面体A′-BCD的体积为
|
圆x2+y2+4x-6y-3=0的圆心坐标为( )
| A、(4,-6) |
| B、(2,-3) |
| C、(-2,3) |
| D、(-4,6) |
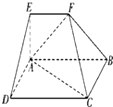 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为