题目内容
已知函数f(x)=(a+1)lnx+x2-x (a∈R),
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)设a>0,如果对任意x1,x2∈(0,+∞),均有f(x1)-f(x2)>3|x1-x2|,求a的取值范围.
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)设a>0,如果对任意x1,x2∈(0,+∞),均有f(x1)-f(x2)>3|x1-x2|,求a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)当a=1时,求函数的导数即可求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数的导数,根据函数单调性和导数之间的关系即可讨论函数f(x)的单调性;
(Ⅲ)将不等式进行转化,即可得到结论.
(Ⅱ)求函数的导数,根据函数单调性和导数之间的关系即可讨论函数f(x)的单调性;
(Ⅲ)将不等式进行转化,即可得到结论.
解答:
解:(I)由题,a=1时,f(1)=0,f′(1)=3,故所求切线方程为3x-y-3=0; …(4分)
(Ⅱ) f(x)定义域为(0,+∞),f′(x)=
+2x-1=
,△=1-8(a+1)=-8a-7,
①a≥-
时,f(x)在(0,+∞)上为增函数;
②-1<a<-
时,f(x)增区间为(0,
),(
,+∞),
减区间为(
,
);
③a≤-1时,f(x)增区间为),(
,+∞),减区间为(0,
);(8分)
( III) 由( II)a>0时,f(x)在(0,+∞)上为增函数,不妨设x1>x2,
则有f(x1)-f(x2)>3(x1-x2),即f(x1)-x1>f(x2)-3x2恒成立,
故y=f(x)-3x在(0,+∞)上为增函数,y′=
+2x-4≥0,
即2
-4≥0,
解得a≥1,
即a的取值范围是[1,+∞).
(Ⅱ) f(x)定义域为(0,+∞),f′(x)=
| a+1 |
| x |
| 2x2-x+a+1 |
| x |
①a≥-
| 7 |
| 8 |
②-1<a<-
| 7 |
| 8 |
1-
| ||
| 4 |
1+
| ||
| 4 |
减区间为(
1-
| ||
| 4 |
1+
| ||
| 4 |
③a≤-1时,f(x)增区间为),(
1+
| ||
| 4 |
1-
| ||
| 4 |
( III) 由( II)a>0时,f(x)在(0,+∞)上为增函数,不妨设x1>x2,
则有f(x1)-f(x2)>3(x1-x2),即f(x1)-x1>f(x2)-3x2恒成立,
故y=f(x)-3x在(0,+∞)上为增函数,y′=
| a+1 |
| x |
即2
| 2(a+1) |
解得a≥1,
即a的取值范围是[1,+∞).
点评:本题主要考查导数的综合应用,考查导数的几何意义以及函数单调性和最值与导数之间的关系,综合性较强,运算量较大.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
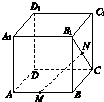 如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设
如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| MN |
| a |
| b |
| c |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
已知a=20.1,b=ln0.1,c=sin1,则( )
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、b>a>c |
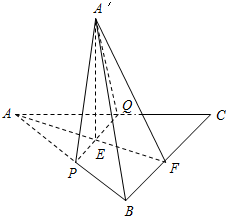 如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为
如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为