题目内容
10.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽调查了500位老人,结果如表所示:| 男 | 女 | |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(1)完成2×2列联表,并根据表中数据,问是否有99%的把握认为该地区的老年人是否需要志愿者帮助与性别有关?
分析 (1)根据表中数据,计算老年人中需要志愿者提供帮助的老年人比例;
(2)补充2×2列联表,计算K2,与临界值比较得出概率结论.
解答 解:(1)根据表中数据知,估计该地区老年人中,需要志愿者提供帮助的老年人的比例为
$\frac{40+30}{40+30+160+270}$=0.14=14%;
(2)补充2×2列联表如下,
| 男 | 女 | 合计 | |
| 需要 | 40 | 30 | 70 |
| 不需要 | 160 | 270 | 430 |
| 合计 | 200 | 300 | 500 |
且9.967>6.635,
所以有99%的把握认为该地区的老年人是否需要志愿者帮助与性别有关.
点评 本题考查了列联表与独立性检验的应用问题,是基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.已知函数y=cos x的定义域为[a,b],值域为[-$\frac{1}{2}$,1],则b-a的值不可能是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
19.已知α,β均为锐角,且$cosα=\frac{{2\sqrt{5}}}{5},cosβ=\frac{{\sqrt{10}}}{10}$,则α-β等于( )
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $-\frac{π}{2}$ |
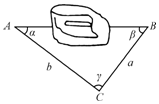 如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.
如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.