题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,角A,B,C成等差数列,则cosB= ;若同时边a,b,c成等比数列,则cos2A= .
考点:正弦定理,余弦定理
专题:三角函数的求值
分析:由A,B,C成等差数列,利用等差数列的性质求出B的度数,即可确定出cosB的值;由a,b,c成等比数列,利用等比数列的性质列出关系式,利用正弦定理化简,将sinB的值代入,利用积化和差公式变形求出2A的度数,即可确定出cos2A的值.
解答:
解:∵A,B,C成等差数列,
∴2B=A+C,
∵A+B+C=π,
∴B=
,
∴cosB=
;
∵a,b,c成等比数列,
∴b2=ac,
利用正弦定理化简得:sin2B=sinAsinC,即sinAsinC=
,
∴sinAsin(
-A)=-
[cos
-cos(2A-
)]=
,
整理得:cos(2A-
)=1,
∴2A-
=kπ(k∈Z),
∴2A=
,
则cos2A=cos
=-
.
故答案为:
;-
∴2B=A+C,
∵A+B+C=π,
∴B=
| π |
| 3 |
∴cosB=
| 1 |
| 2 |
∵a,b,c成等比数列,
∴b2=ac,
利用正弦定理化简得:sin2B=sinAsinC,即sinAsinC=
| 3 |
| 4 |
∴sinAsin(
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| 4 |
整理得:cos(2A-
| 2π |
| 3 |
∴2A-
| 2π |
| 3 |
∴2A=
| 2π |
| 3 |
则cos2A=cos
| 2π |
| 3 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了正弦定理,等差、等比数列的性质,数列掌握正弦定理是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
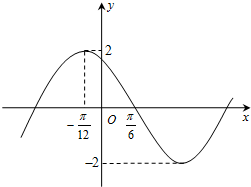 已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )
已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(6x-
| ||
D、f(x)=2sin(6x+
|
已知集合M={x|-2≤x≤8},n={x|x2-3x+2≤0},在集合M中任取一个元素x,则“x∈M∩N”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若不等式log2(|x+1|+|x-2|-m)≥2恒成立,则实数m的取值范围为( )
| A、(-∞,-3] |
| B、[-3,-1] |
| C、[-1,3] |
| D、(-∞,-1] |