题目内容
△ABC的内角A,B,C所对的边分别为a,b,c.已知
=(2a-b-c,2a-b-c),
=(sinA+sinB,-sinC),若
⊥
且sinB=2sinC.
(Ⅰ)判断△ABC的形状;
(Ⅱ)求cos(2B+
)的值.
| m |
| n |
| m |
| n |
(Ⅰ)判断△ABC的形状;
(Ⅱ)求cos(2B+
| π |
| 6 |
考点:三角形的形状判断,两角和与差的余弦函数
专题:三角函数的求值
分析:(Ⅰ)利用向量的数量积的坐标运算及正弦定理可得a=
c,再由余弦定理可得cosB=
=-
<0,从而可判断△ABC为钝角三角形;
(Ⅱ)由(Ⅰ)知,cosB=-
,则sinB=
,利用二倍角公式可求得cos2B的值,再利用两角和的余弦即可求得cos(2B+
)的值.
| 3 |
| 2 |
c2+
| ||
2c•
|
| 1 |
| 4 |
(Ⅱ)由(Ⅰ)知,cosB=-
| 1 |
| 4 |
| ||
| 4 |
| π |
| 6 |
解答:
解:(Ⅰ)由
⊥
得:
•
=0,即(2a-b-c)(sinA+sinB-sinC)=0,…1分
由正弦定理得:(2a-b-c)(a+b-c)=0,…2分
而a+b-c>0,故2a-b-c=0…3分
又sinB=2sinC得:b=2c,因此a=
c…4分
由于cosB=
=-
<0,所以
<B<π,故△ABC为钝角三角形…6分
(Ⅱ)由(Ⅰ)知,cosB=-
,则sinB=
…8分
故cos2B=2×(-
)2-1=-
,sin2B=2×
×(-
)=-
…10分
因此cos(2B+
)=(-
)×
-(-
)×
=
…12分
| m |
| n |
| m |
| n |
由正弦定理得:(2a-b-c)(a+b-c)=0,…2分
而a+b-c>0,故2a-b-c=0…3分
又sinB=2sinC得:b=2c,因此a=
| 3 |
| 2 |
由于cosB=
c2+
| ||
2c•
|
| 1 |
| 4 |
| π |
| 2 |
(Ⅱ)由(Ⅰ)知,cosB=-
| 1 |
| 4 |
| ||
| 4 |
故cos2B=2×(-
| 1 |
| 4 |
| 7 |
| 8 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 8 |
因此cos(2B+
| π |
| 6 |
| 7 |
| 8 |
| ||
| 2 |
| ||
| 8 |
| 1 |
| 2 |
| ||||
| 16 |
点评:本题考查三角形形状的判断,考查两角和与差的余弦函数,考查数量积的坐标运算与余弦定理的由于,考查运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个箱子中装有9张卡片,分别标有数字1,2,3,…,9,现在有放回地依次抽取3张,然后按抽取的先后顺序依次构成一个三位数,则这三位数中恰有两个数字重复的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
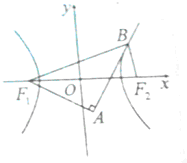 如图,F1,F2分别是双曲线
如图,F1,F2分别是双曲线