题目内容
已知函数f(x)=ax2+blnx在x=1处有极值
.
(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
| 1 |
| 2 |
(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)根据条件,建立方程关系即可求a,b的值;
(2)求函数的导数,利用函数导数和函数单调性的关系,即可求f(x)的单调区间.
(2)求函数的导数,利用函数导数和函数单调性的关系,即可求f(x)的单调区间.
解答:
解:(1)∵f(x)=ax2+blnx在x=1处有极值
,
∴f(1)=a=
,即a=
,
函数的导数f′(x)=2ax+
,
∴f′(1)=2a+b=0,解得b=-1,
即a=
,b=-1.
(2)∵f(x)=
x2-lnx;函数的定义域为(0,+∞),
∴f′(x)=x-
=
由f′(x)=0,解得x=1,
当x>1时,f′(x)>0,此时函数单调递增,
当0<x<1时,f′(x)<0,此时函数单调递减,
即函数的单调递减区间为(0,1),单调递增区间为(1,+∞).
| 1 |
| 2 |
∴f(1)=a=
| 1 |
| 2 |
| 1 |
| 2 |
函数的导数f′(x)=2ax+
| b |
| x |
∴f′(1)=2a+b=0,解得b=-1,
即a=
| 1 |
| 2 |
(2)∵f(x)=
| 1 |
| 2 |
∴f′(x)=x-
| 1 |
| x |
| x2-1 |
| x |
由f′(x)=0,解得x=1,
当x>1时,f′(x)>0,此时函数单调递增,
当0<x<1时,f′(x)<0,此时函数单调递减,
即函数的单调递减区间为(0,1),单调递增区间为(1,+∞).
点评:本题主要考查函数的单调性和导数之间的关系,根据条件求出a,b,c的值是解决本题的关键,考查学生的运算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
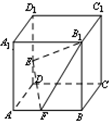 (理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是
(理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是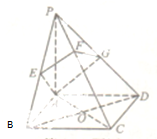 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,过A点的截面AEFG分别交PB,PC,PD于点E,F,G,且PB⊥AE,PD⊥AG.下列结论正确的是
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,过A点的截面AEFG分别交PB,PC,PD于点E,F,G,且PB⊥AE,PD⊥AG.下列结论正确的是