题目内容
在直角坐标系xoy中,已知曲线M:
(t为参数)与曲线N:
(θ为参数)相交于两个点A,B,则线段AB的长为 .
|
|
考点:点的极坐标和直角坐标的互化,参数方程化成普通方程
专题:直线与圆,坐标系和参数方程
分析:把参数方程化为普通方程,求出圆心到直线的距离d,再由弦长公式求得弦长AB的值.
解答:
解:在直角坐标系xOy中,已知曲线M:
,(t为参数),
消去参数t,化为直角坐标方程为 2x+y-5=0.
曲线N:
(θ为参数),即 x2+y2=16,表示以原点为圆心、半径等于4的圆.
由于圆心到直线的距离为 d=
=
,由弦长公式可得弦长AB=2
=2
=2
.
故答案为:2
.
|
消去参数t,化为直角坐标方程为 2x+y-5=0.
曲线N:
|
由于圆心到直线的距离为 d=
| |0+0-5| | ||
|
| 5 |
| r2-d2 |
| 16-5 |
| 11 |
故答案为:2
| 11 |
点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,弦长公式的应用,属于中档题.

练习册系列答案
相关题目
 如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°.
如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°.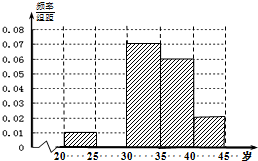 对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:
对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得: