题目内容
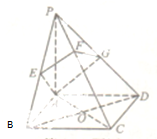 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,过A点的截面AEFG分别交PB,PC,PD于点E,F,G,且PB⊥AE,PD⊥AG.下列结论正确的是
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,过A点的截面AEFG分别交PB,PC,PD于点E,F,G,且PB⊥AE,PD⊥AG.下列结论正确的是①BD∥平面AEFG;
②PC⊥平面AEFG;
③EF∥平面PAD;
④点A,B,C,D,E,F,G在同一球面上;
⑤若PA=AB=1,则四棱锥O-AEFG的体积为
| 1 |
| 9 |
考点:空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离
分析:①证明EG∥BD,可得结论;②证明AE⊥PC,AG⊥PC,即可证明PC⊥平面AEFG;③利用反证法可以得出结论;
④由②可知OA=OB=OC=OD=OE=OF=OG=
AC,故点A,B,C,D,E,F,G在同一球面上;⑤若连接AF,取AF的中点M,连接OM,可求四棱锥O-AEFG的体积.
④由②可知OA=OB=OC=OD=OE=OF=OG=
| 1 |
| 2 |
解答:
解:∵PB⊥AE,PD⊥AG,AB=AD,∴PB=PD,PE=PG,∴EG∥BD,∴BD∥平面AEFG,∴①正确;
由已知可得BC⊥平面PAB,CD⊥平面PAD,∴AE⊥BC,AG⊥CD,∵PB⊥AE,PD⊥AG,∴AE⊥PC,AG⊥PC,
∴PC⊥平面AEFG,∴②正确;
由②可知EF⊥PC,∴EF与BC必相交,假设EF∥平面PAD,由BC∥平面PAD,可得平面PAD∥平面PBC,显然矛盾,∴③错误;
由②可知OA=OB=OC=OD=OE=OF=OG=
AC,∴点A,B,C,D,E,F,G在同一球面上,∴④正确;
连接AF,取AF的中点M,连接OM,则OM∥PC,∴OM⊥平面AEFG,由已知可得AE=
,AF=
,∴EF=
,OM=
,∴四棱锥O-AEFG的体积V=
=
,∴⑤错误.
故答案为:①②④.
由已知可得BC⊥平面PAB,CD⊥平面PAD,∴AE⊥BC,AG⊥CD,∵PB⊥AE,PD⊥AG,∴AE⊥PC,AG⊥PC,
∴PC⊥平面AEFG,∴②正确;
由②可知EF⊥PC,∴EF与BC必相交,假设EF∥平面PAD,由BC∥平面PAD,可得平面PAD∥平面PBC,显然矛盾,∴③错误;
由②可知OA=OB=OC=OD=OE=OF=OG=
| 1 |
| 2 |
连接AF,取AF的中点M,连接OM,则OM∥PC,∴OM⊥平面AEFG,由已知可得AE=
| ||
| 2 |
| ||
| 3 |
| ||
| 6 |
| ||
| 3 |
| AE•EF•OM |
| 3 |
| 1 |
| 18 |
故答案为:①②④.
点评:本题考查空间中直线与直线之间的位置关系,考查学生分析解决问题的能力,难度中等.

练习册系列答案
相关题目
设某离散型随机变量ξ的概率分布列如下表,则p的值为( )
| ξ | 1 | 2 | 3 | 4 | ||||||
| P |
|
|
|
p |
A、
| ||
B、
| ||
C、
| ||
D、
|
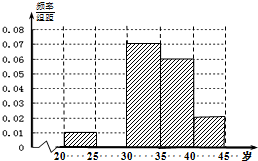 对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:
对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得: