题目内容
设向量
=（1，2），
=（2，1），若向量λ
+
与向量
=（-3，3）垂直，则λ= ．
| a |
| b |
| a |
| b |
| c |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由题意，先求出向量λ
+
的坐标，再由垂直的条件得到λ的方程，解方程求值即可．
| a |
| b |
解答：
解：∵
=（1，2），
=（2，1），
∴λ
+
=（λ+2，2λ+1），又向量λ
+
与向量
=（-3，3）垂直，
∴-3λ-6+6λ+3=0，解得λ=1．
故答案为：1．
| a |
| b |
∴λ
| a |
| b |
| a |
| b |
| c |
∴-3λ-6+6λ+3=0，解得λ=1．
故答案为：1．
点评：本题考查数量积的运算，向量坐标表示的运算，向量垂直的条件，属于向量基础题，必会型．
练习册系列答案
全能测控期末小状元系列答案
相关题目
命题“如果实数x能被2整除，则x是偶数”的否命题是（ ）
| A、如果实数x不能被2整除，则x是偶数 |
| B、如果实数x能被2整除，则x不是偶数 |
| C、如果实数x不能被2整除，则x不是偶数 |
| D、存在一个能被2整除的数，它不是偶数 |
已知全集U=R，M={x|x＞1}，N={x|x≤-1，或x≥5}，则M∩（∁UN）=（ ）
| A、{x|1＜x≤5} |
| B、{x|1＜x＜5} |
| C、{x|-1＜x＜5} |
| D、∅ |
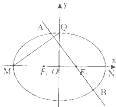已知椭圆C：