Question

已知函数f（x）=

ax

ex

，a≠0．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当a=1时，已知x₁＜x₂，且f（x₁）=f（x₂），求证：f（x₁）＞f（2-x₂）

Answer 1

考点：利用导数研究函数的单调性,函数单调性的性质

专题：函数的性质及应用,导数的综合应用

分析：（1）f′(x)=

aex-axex

(ex)2

=

a(1-x)

ex

，令f′（x）=0，得x=1，再分a＞0时与a＜0时，讨论f′（x）＞0或f′（x）＜0，进一步可得函数的单调区间．
（2）画函数f（x）的图象，找出x₁＜1，x₂＞1，要证f（x₁）＞f（2-x₂）只要证明x₂＞1时f（x₂）-f（2-x₂）＞0即可，
构造函数g（x）=f（x）-f（2-x），即g（x）=

x

ex

-

2-x

e2-x

，只要证明对于?x＞1，g（x）＞0恒成立即可．

解答： 解：（1）f′(x)=

aex-axex

(ex)2

=

a(1-x)

ex

，令f′（x）=0，得x=1，
当a＞0时，如果x∈（1，+∞），那么f′（x）＜0，因此（1，+∞）为函数的单调减区间；如果x∈（-∞，1），那么f′（x）＞0，因此（-∞，1）为函数的单调增区间．
当a＜0时，如果x∈（1，+∞），那么f′（x）＞0，因此（1，+∞）为函数的单调增区间；如果x∈（-∞，1），那么f′（x）＜0，因此（-∞，1）为函数的单调减区间．
（2）当a=1时，f（x）=

x

ex

，由（1）知，（1，+∞）为函数的单调减区间；（-∞，1）为函数的单调增区间．
又f（0）=0，f（1）=

1

e

，函数f（x）的图象：

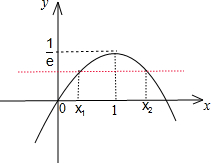
∵x₁＜x₂，且f（x₁）=f（x₂），∴从图象上看，x₁＜1，x₂＞1，
f（x₁）＞f（2-x₂）?f（x₂）＞f（2-x₂），∴要证f（x₁）＞f（2-x₂）只要证明x₂＞1时f（x₂）-f（2-x₂）＞0即可：
构造函数g（x）=f（x）-f（2-x），即g（x）=

x

ex

-

2-x

e2-x

，下面证明：对于?x＞1，g（x）＞0恒成立，
则g′（x）=

1-x

ex

-

1-x

e2-x

=

(1-x)(1-e2(x-1))

ex

，
如果x∈（1，+∞），那么x-1＞0，e^2（x-1）＞1，则（1-x）（1-e^2（x-1））＞0，因此g′（x）＞0，因此g（x）在（1，+∞）上为单调增函数；
∴g（x）在（1，+∞）上单调递增，
在x∈[1，+∞）时：当x=1时，函数g（x）取最小值，即g最小值=g(1)=

1

e

-

2-1

e2-1

=0，∴对于?x∈（1，+∞），g（x）＞0恒成立，
∴x₂＞1时f（x₂）-f（2-x₂）＞0，∴f（x₂）＞f（2-x₂），
又∵f（x₁）=f（x₂），
∴f（x₁）＞f（2-x₂）．

点评：本题重在考查函数与导数的综合应用，对于较复杂的问题可以构造函数，然后利用导数去研究函数的单调性，从而使问题得以解决，属于高档题．