Question

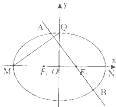已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的长轴左右端点M，N与短轴上端点Q构成的三角形的面积为2

3

，离心率e=

1

2

．
（Ⅰ）求椭圆的方程．
（Ⅱ）若过椭圆C右焦点F₂作垂直于线段MQ的直线L，交椭圆C于A，B两点，求四边形AMBQ面积S．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）利用椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的长轴左右端点M，N与短轴上端点Q构成的三角形的面积为2

3

，离心率e=

1

2

，建立方程，求出a，b，即可求椭圆的方程．
（Ⅱ）求出直线L的方程，代入椭圆方程，利用韦达定理求出|AB|，再计算四边形AMBQ面积S．

解答： 解：（Ⅰ）∵椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的长轴左右端点M，N与短轴上端点Q构成的三角形的面积为2

3

，离心率e=

1

2

，
∴

ab=2 3 c a = 1 2

------------（2分）
∴a=2，b=

3

------------（4分）
∴椭圆的方程为

x2

4

+

y2

3

=1------------（5分）
（Ⅱ）由（Ⅰ）知F₂（1，0），M（-2，0），Q（0，

3

）------------（6分）
∴直线MQ斜率为

3

2

，
又∵L⊥MQ，∴直线L斜率k=-

2

3

------------（7分）
直线L：y=-

2

3

（x-1）------------（8分）
代入椭圆方程得25x²-32x-20=0------------（9分）
设A（x₁，y₁），B（x₂，y₂）
由韦达定理x₁+x₂=

32

25

，x₁x₂=-

20

25

------------（10分）
∴|AB|=

1+ 4 3

•

( 32 25 )2+ 80 25

=

84

25

------------（11分）
∴四边形AMBQ面积S=

|AB||MQ|

2

=

42 7

25

．------------（12分）

点评：本题考查椭圆的方程与性质，考查直线与椭圆的位置关系，考查学生的计算能力，属于中档题．