题目内容
设△ABC的内角A、B、C的对边分别为a、b、c，若tanC=
且c=
，求△ABC的面积的最大值．
| sinA+sinB |
| cosA+cosB |
| ||
| 2 |
考点：正弦定理
专题：解三角形
分析：依题意，可求得C=
，利用余弦定理与基本不等式可得ab≤
，从而可求得△ABC的面积的最大值．
| π |
| 3 |
| 3 |
| 4 |
解答：
解：∵tanC=
=
，
∴sinCcosA+sinCcosB=sinAcosC+sinBcosC，
整理得：sin（C-A）=sin（B-C），
∵A、B、C为△ABC的内角，
∴C-A=B-C或C-A=π-（B-C）（舍），
∴C=
，又c=
，
由余弦定理得：
=c2=a2+b2-2abcosC≥2ab-2ab×
=ab，
即ab≤
（当且仅当a=b时取等号），
∴S△ABC=
absinC≤
×
×
=
．
| sinC |
| cosC |
| sinA+sinB |
| cosA+cosB |
∴sinCcosA+sinCcosB=sinAcosC+sinBcosC，
整理得：sin（C-A）=sin（B-C），
∵A、B、C为△ABC的内角，
∴C-A=B-C或C-A=π-（B-C）（舍），
∴C=
| π |
| 3 |
| ||
| 2 |
由余弦定理得：
| 3 |
| 4 |
| 1 |
| 2 |
即ab≤
| 3 |
| 4 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| ||
| 2 |
3
| ||
| 16 |
点评：本题考查两角差的正弦与正弦定理的综合应用，考查基本不等式与三角形的面积公式，考查转化思想与运算能力，属于中档题．
练习册系列答案
相关题目
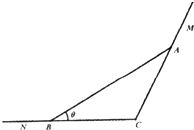如图，用木板AB借助墙角MCN转成一个三角形ABC区域，用以堆放谷物，已知∠MCN=
