题目内容
自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段、EF段、GH段都是易堵车路段,假设这三条路段堵车与否相互独立,这三条路段的堵车概率及平均堵车时间如表1所示.
表1:
经调查发现,堵车概率x在(
,1)上变化,y在(0,
)上变化.
在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计CD段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
表2:
(Ⅰ)求CD段平均堵车时间a的值;
(Ⅱ)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
表1:
| CD段 | EF段 | GH段 | |||
| 堵车概率 | x | y |
| ||
| 平均堵车时间 (单位:小时) |
a | 2 | 1 |
| 2 |
| 3 |
| 1 |
| 2 |
在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计CD段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
表2:
| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1,2] | 6 |
| (2,3] | 38 |
| (3,4] | 24 |
| (4,5] | 24 |
(Ⅱ)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
考点:几何概型,相互独立事件的概率乘法公式,离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:(Ⅰ)利用组中值,可求CD段平均堵车时间a的值;
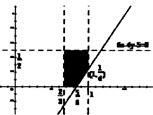
(Ⅱ)求出走乙路线花汽油费的数学期望是40y+550元,可得选择走甲线路应满足(550+4y)-[500(1-x)+(500+60)x]≥0,即6x-4y-5≤0,利用面积之比,求出选择走甲线路的概率.
(Ⅱ)求出走乙路线花汽油费的数学期望是40y+550元,可得选择走甲线路应满足(550+4y)-[500(1-x)+(500+60)x]≥0,即6x-4y-5≤0,利用面积之比,求出选择走甲线路的概率.
解答:
 解:(Ⅰ)a=0.5×
解:(Ⅰ)a=0.5×
+1.5×
+2.5×
+3.5×
+4.5×
=3;
(Ⅱ)在EF路段多花汽油费的数学期望是20×2y=40y元,在GH路段多花汽油费的数学期望是20×1×
=5元,
∵EF,GH路段堵车与否相互独立,
∴走乙路线多花汽油费的数学期望是40y+5元,
∴走乙路线花汽油费的数学期望是40y+550元,
∴选择走甲线路应满足(550+4y)-[500(1-x)+(500+60)x]≥0,即6x-4y-5≤0,
∵x在(
,1)上变化,y在(0,
)上变化,
∴选择走甲线路的概率为
=
 解:(Ⅰ)a=0.5×
解:(Ⅰ)a=0.5×| 8 |
| 100 |
| 6 |
| 100 |
| 38 |
| 100 |
| 24 |
| 100 |
| 24 |
| 100 |
(Ⅱ)在EF路段多花汽油费的数学期望是20×2y=40y元,在GH路段多花汽油费的数学期望是20×1×
| 1 |
| 4 |
∵EF,GH路段堵车与否相互独立,
∴走乙路线多花汽油费的数学期望是40y+5元,
∴走乙路线花汽油费的数学期望是40y+550元,
∴选择走甲线路应满足(550+4y)-[500(1-x)+(500+60)x]≥0,即6x-4y-5≤0,
∵x在(
| 2 |
| 3 |
| 1 |
| 2 |
∴选择走甲线路的概率为
(1-
| ||||||||||
(1-
|
| 7 |
| 8 |
点评:本题考查概率的计算,考查面积的计算,属于中档题.

练习册系列答案
相关题目
函数y=2sin(2x+
)的一条对称轴是( )
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
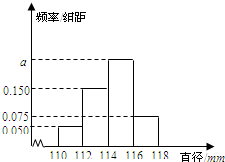 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.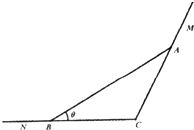 如图,用木板AB借助墙角MCN转成一个三角形ABC区域,用以堆放谷物,已知∠MCN=
如图,用木板AB借助墙角MCN转成一个三角形ABC区域,用以堆放谷物,已知∠MCN=