题目内容
4.在某校,一学科的学习由必修、选修两门课程组成,对某层次学生调查统计知,有且仅有一门课程获得学分概率为$\frac{5}{12}$,至少一门课程获得学分的概率为$\frac{11}{12}$.规定两门课程都获得学分该学科才能结业.已知必修课程获得学分的概率大于选修课程获得学分的概率且互不影响.(1)对该层内的A同学,该学科能结业的概率是多少?
(2)在该层次的同学中随机抽取5名,记X为其中能结业的学生数,求X的期望EX与方差DX.
分析 (1)设该层内的任意一同学必修课程获得学分的概率为p,选修课程获得学分的概率为q,则(1-p)q+p(1-q)=$\frac{5}{12}$,1-(1-p)(1-q)=$\frac{11}{12}$,联立解得pq即可得出.
(2)由题意可得:X~B$(5,\frac{1}{2})$,即可得出E(X),D(X).
解答 解:(1)设该层内的任意一同学必修课程获得学分的概率为p,选修课程获得学分的概率为q,
则(1-p)q+p(1-q)=$\frac{5}{12}$,1-(1-p)(1-q)=$\frac{11}{12}$,
联立解得pq=$\frac{1}{2}$.
∴该学科能结业的概率为$\frac{1}{2}$.
(2)由题意可得:X~B$(5,\frac{1}{2})$,E(X)=5×$\frac{1}{2}$=$\frac{5}{2}$.D(X)=5×$\frac{1}{2}×(1-\frac{1}{2})$=$\frac{5}{4}$.
点评 本题考查了二项分布列的概率与数学期望计算公式及其性质、相互独立及其对立事件的概率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.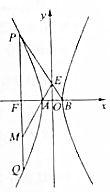 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
15.已知函数f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x),x∈R,则f(x)是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
19.设集合$A=[(x,y)|\frac{x^2}{25}+\frac{y^2}{16}≤1],B=[(x,y)|\left\{\begin{array}{l}|x|≤m\\|y|≤n\end{array}\right.,0<m<5,0<n<4且(m,n)∈A]$,则集合∁AB对应图形面积取得最小值时,m+n的值为( )
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
9.已知直角△ABC中,AB=3,AC=4,BC=5,I是△ABC的内心,P是△IBC内部(不含边界)的动点,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的取值范围是( )
| A. | ($\frac{7}{12}$,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{4}$,$\frac{7}{12}$) | D. | ($\frac{1}{4}$,1) |
6.在△ABC中,A1,B1分别是边BA,CB的中点,A2,B2分别是线段A1A,B1B的中点,…,An,Bn分别是线段${A_{n-1}}A,{B_{n-1}}B(n∈{N^*},n>1)$的中点,设数列{an},{bn}满足:向量$\overrightarrow{{B_n}{A_n}}={a_n}\overrightarrow{CA}+{b_n}\overrightarrow{CB}(n∈{N^*})$,有下列四个命题,其中假命题是( )
| A. | 数列{an}是单调递增数列,数列{bn}是单调递减数列 | |
| B. | 数列{an+bn}是等比数列 | |
| C. | 数列$\{\frac{a_n}{b_n}\}$有最小值,无最大值 | |
| D. | 若△ABC中,C=90°,CA=CB,则$|\overrightarrow{{B_n}{A_n}}|$最小时,${a_n}+{b_n}=\frac{1}{2}$ |
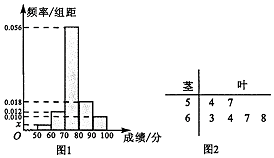 某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.