题目内容
3．已知$\vec a$与$\vec b$的夹角为$\frac{2π}{3}$，且$|\vec a|=2$，$|\vec b|=5$，则$（2\vec a-\vec b）•\vec a$=13．分析 利用平面向量的数量积定义计算$\overrightarrow{a}•\overrightarrow{b}$，${\overrightarrow{a}}^{2}$，将$（2\vec a-\vec b）•\vec a$展开即可得出答案．
解答 解：$\overrightarrow{a}•\overrightarrow{b}$=2×5×cos$\frac{2π}{3}$=-5，${\overrightarrow{a}}^{2}$=4，
∴$（2\vec a-\vec b）•\vec a$=2${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=8+5=13．
故答案为：13．
点评 本题考查了平面向量的数量积运算，属于基础题．
练习册系列答案
相关题目
13．定义在R上的奇函数f（x）满足：f（x+1）=f（x-1），且当-1＜x＜0时，f（x）=2x-1，则f（log220）等于（ ）
| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | -$\frac{1}{5}$ | D． | $\frac{1}{5}$ |
14．
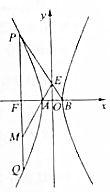已知O为坐标原点，F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，A，B分别为左、右顶点，过点F做x轴的垂线交双曲线于点P，Q，连接PB交y轴于点E，连结AE交QF于点M，若M是线段QF的中点，则双曲线C的离心率为（ ）
已知O为坐标原点，F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，A，B分别为左、右顶点，过点F做x轴的垂线交双曲线于点P，Q，连接PB交y轴于点E，连结AE交QF于点M，若M是线段QF的中点，则双曲线C的离心率为（ ）| A． | 2 | B． | $\frac{5}{2}$ | C． | 3 | D． | $\frac{7}{2}$ |
11．（理）设θ为直线$x-\sqrt{3}y-1=0$的倾斜角，则$sin（θ+\frac{π}{4}）$=（ ）
| A． | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B． | $\frac{{\sqrt{6}+1}}{4}$ | C． | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D． | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
18．已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$，N={x|-1＜x＜1}，则（ ）
| A． | M?N | B． | N?M | C． | M=N | D． | M∩N=∅ |
8．运行如图所示的程序框图，输出的n等于（ ）
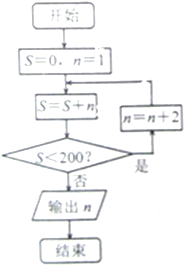
| A． | 30零 | B． | 29 | C． | 28 | D． | 27 |
15．已知函数f（x）=sin（$\frac{π}{3}$-2x）-$\sqrt{3}$sin（$\frac{π}{6}$+2x），x∈R，则f（x）是（ ）
| A． | 最小正周期为π的偶函数 | B． | 最小正周期为2π的奇函数 | ||
| C． | 最小正周期为π的奇函数 | D． | 最小正周期为2π的偶函数 |
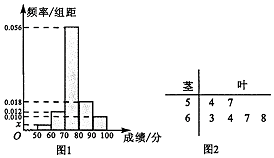某省2016年高中数学学业水平测试的原始成绩采用百分制，发布成绩使用等级制．各等级划分标准为：85分及以上，记为A等；分数在[70，85）内，记为B等；分数在[60，70）内，记为C等；60分以下，记为D等．同时认定A，B，C为合格，D为不合格．已知甲，乙两所学校学生的原始成绩均分布在[50，100]内，为了比较两校学生的成绩，分别抽取50名学生的原始成绩作为样本进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出甲校的样本频率分布直方图如图1所示，乙校的样本中等级为C，D的所有数据的茎叶图如图2所示．
6．在△ABC中，A1，B1分别是边BA，CB的中点，A2，B2分别是线段A1A，B1B的中点，…，An，Bn分别是线段${A_{n-1}}A，{B_{n-1}}B（n∈{N^*}，n＞1）$的中点，设数列{an}，{bn}满足：向量$\overrightarrow{{B_n}{A_n}}={a_n}\overrightarrow{CA}+{b_n}\overrightarrow{CB}（n∈{N^*}）$，有下列四个命题，其中假命题是（ ）
| A． | 数列{an}是单调递增数列，数列{bn}是单调递减数列 | |
| B． | 数列{an+bn}是等比数列 | |
| C． | 数列$\{\frac{a_n}{b_n}\}$有最小值，无最大值 | |
| D． | 若△ABC中，C=90°，CA=CB，则$|\overrightarrow{{B_n}{A_n}}|$最小时，${a_n}+{b_n}=\frac{1}{2}$ |