题目内容
10.某经销商试销A、B两种商品一个月(30天)的记录如下:| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
分析 (1)根据题意可得频率,进而得到X,Y的分布列,利用相互独立事件的概率计算公式即可得出
P(X>100,Y>100).
(2)利用数学期望与方差的计算公式即可得出.
解答 解:(1)根据题意可得:X的分布列如下:
| X | 0 | 40 | 80 | 120 | 160 | 200 |
| P | $\frac{3}{30}$ | $\frac{5}{30}$ | $\frac{7}{30}$ | $\frac{7}{30}$ | $\frac{5}{30}$ | $\frac{3}{30}$ |
| Y | 0 | 40 | 80 | 120 | 160 | 200 |
| P | $\frac{4}{30}$ | $\frac{4}{30}$ | $\frac{6}{30}$ | $\frac{8}{30}$ | $\frac{5}{30}$ | $\frac{3}{30}$ |
(2)E(X)=$0×\frac{3}{30}$+$40×\frac{5}{30}$+80×$\frac{7}{30}$+$120×\frac{7}{30}$+160×$\frac{5}{30}$+200×$\frac{3}{30}$=100.
E(Y)=0×$\frac{4}{30}$+$40×\frac{4}{30}$+$80×\frac{6}{30}$+120×$\frac{8}{30}$+160×$\frac{5}{30}$+200×$\frac{3}{30}$=100.
∴两种商品日获利值均值都是100元.
D(X)=1002×$\frac{3}{30}$+602×$\frac{5}{30}$+202×$\frac{7}{30}$+$2{0}^{2}×\frac{7}{30}$+602×$\frac{5}{30}$+1002×$\frac{3}{30}$=$\frac{10160}{3}$.
D(Y)=1002×$\frac{4}{30}$+602×$\frac{4}{30}$+202×$\frac{6}{30}$+202×$\frac{8}{30}$+602×$\frac{5}{30}$+1002×$\frac{3}{30}$=$\frac{10800}{3}$.
∵D(X)<D(Y),
∴应选择A商品.
点评 本题考查了相互独立事件的概率计算公式、随机变量的数学期望与方差的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.五个人负责一个社团的周一至周五的值班工作,每人一天,则甲同学不值周一,乙同学不值周五,且甲,乙不相邻的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
18.已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$,N={x|-1<x<1},则( )
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |
15.已知函数f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x),x∈R,则f(x)是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
2.命题“若a>b,则a+c>b+c”的逆命题是( )
| A. | 若a>b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a≤b,则a+c≤b+c |
19.设集合$A=[(x,y)|\frac{x^2}{25}+\frac{y^2}{16}≤1],B=[(x,y)|\left\{\begin{array}{l}|x|≤m\\|y|≤n\end{array}\right.,0<m<5,0<n<4且(m,n)∈A]$,则集合∁AB对应图形面积取得最小值时,m+n的值为( )
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
13. 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
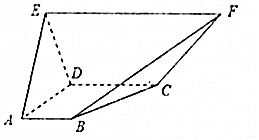 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.