题目内容
20. 已知双曲线C1:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为x+2y=0,且点(2,$\sqrt{2}$)在双曲线C1上.
已知双曲线C1:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为x+2y=0,且点(2,$\sqrt{2}$)在双曲线C1上.(1)求双曲线C1的标准方程;
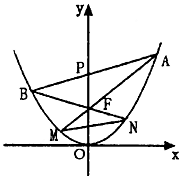
(2)设抛物线C2:x2=2py(p>0)的焦点F是双曲线C1的一个顶点,过点P(0,t)(t>0)任意作一条直线交抛物线于两点A,B,直线AF,BF与抛物线的另一交点分别为M,N.若直线MN的斜率为k1,直线AB的斜率为k2.问:是否存在实数t,使得k1=2k2恒成立?若存在,求t的值,若不存在,说明理由.
分析 (1)根据渐近线方程求得b=2a,将点(2,$\sqrt{2}$)代入抛物线方程,即可求得a和b的值,即可求得双曲线C1的标准方程;
(2)由(1)求得抛物线方程,设直线AB的方程为:y=k1x+t,直线AF的方程为y=nx+1,代入抛物线方程,由韦达定理,直线的斜率公式k1=-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{t}$k2.
解答 解:(1)由题意可知:双曲线焦点在x轴上,渐近线方程y=±$\frac{a}{b}$x,则$\frac{a}{b}$=$\frac{1}{2}$,b=2a,
将点(2,$\sqrt{2}$)代入双曲线方程:$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{4{a}^{2}}=1$,即可求得a=1,则b=2,
∴双曲线方程为:${y}^{2}-\frac{{x}^{2}}{4}=1$;
(2)存在实数t,使得k1=2k2,由(1)可知,抛物线方程C2的焦点F(0,1),则方程为x2=4y,
由题意可知:设直线AB的方程为:y=k1x+t,
$\left\{\begin{array}{l}{y={k}_{2}x+1}\\{{x}^{2}=4y}\end{array}\right.$,消去y,x2-4k2x-4t=0,设A(x1,y1),B(x2,y2),
由韦达定理可知:x1+x2=4k2,x1x2=-4t,
设直线AF,BF分别于抛物线交于M(x3,y3),N(x4,y4),
则k1=$\frac{{y}_{3}-{y}_{4}}{{x}_{3}-{x}_{4}}$=$\frac{\frac{{x}_{3}^{2}}{4}-\frac{{x}_{4}^{2}}{4}}{{x}_{3}-{x}_{4}}$=$\frac{{x}_{3}+{x}_{4}}{4}$,
设直线AF的方程为y=nx+1,
则$\left\{\begin{array}{l}{y=nk+1}\\{{x}^{2}=4y}\end{array}\right.$,消去y,整理得:x2-4nx-4=0.,则x1x3=-4,
同理可得:x2x4=-4,
故k1=$\frac{{x}_{3}+{x}_{4}}{4}$=-$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{1}{t}$k2,
∴存在实数t=$\frac{1}{2}$,使得k1=2k2恒成立.
点评 本题考查双曲线的简单几何性质,考查直线与抛物线的位置关系,考查韦达定理,考查计算能力,属于中档题.

| A. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}+1}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
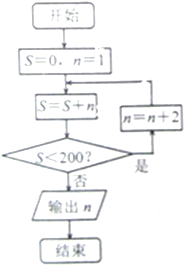
| A. | 30零 | B. | 29 | C. | 28 | D. | 27 |
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |

| A. | $\frac{1}{9}$ | B. | -1或1 | C. | -l | D. | l |
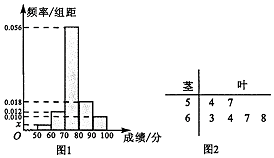 某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.