题目内容
18.设f(x)=ex,f(x)=g(x)-h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[-1,1]时,不等式mg(x)+h(x)≥0成立,则m的最小值为( )| A. | $\frac{{e}^{2}-1}{{e}^{2}+1}$ | B. | $\frac{2}{{e}^{2}+1}$ | C. | $\frac{{e}^{2}+1}{{e}^{2}-1}$ | D. | $\frac{1-{e}^{2}}{1+{e}^{2}}$ |
分析 由F(x)=g(x)+h(x)及g(x),h(x)的奇偶性可求得g(x),h(x),进而可把mg(x)+h(x)≥0表示出来,分离出参数后,求函数的最值问题即可解决.
解答 解:由f(x)=g(x)-h(x),即ex=g(x)-h(x)①,得e-x=g(-x)-h(-x),
又g(x),h(x)分别为偶函数、奇函数,所以e-x=g(x)+h(x)②,
联立①②解得,g(x)=$\frac{1}{2}$(ex+e-x),h(x)=$\frac{1}{2}$(ex-e-x).
mg(x)+h(x)≥0,即m•$\frac{1}{2}$(ex+e-x)+$\frac{1}{2}$(ex-e-x)≥0,也即m≥$\frac{{e}^{-x}-{e}^{x}}{{e}^{x}+{e}^{-x}}$,即m≥1-$\frac{2}{1+{e}^{-2x}}$
∵存在实数m,当x∈[-1,1]时,不等式mg(x)+h(x)≥0成立,1-$\frac{2}{1+{e}^{-2x}}$≥$\frac{{e}^{2}-1}{{e}^{2}+1}$,∴m≥$\frac{{e}^{2}-1}{{e}^{2}+1}$.
∴m的最小值为$\frac{{e}^{2}-1}{{e}^{2}+1}$.
故选A.
点评 本题考查函数的奇偶性、单调性及函数恒成立问题,考查学生综合运用所学知识分析问题解决问题的能力,本题综合性强,难度大.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
15.已知函数f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x),x∈R,则f(x)是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
9.已知直角△ABC中,AB=3,AC=4,BC=5,I是△ABC的内心,P是△IBC内部(不含边界)的动点,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的取值范围是( )
| A. | ($\frac{7}{12}$,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{4}$,$\frac{7}{12}$) | D. | ($\frac{1}{4}$,1) |
6.在△ABC中,A1,B1分别是边BA,CB的中点,A2,B2分别是线段A1A,B1B的中点,…,An,Bn分别是线段${A_{n-1}}A,{B_{n-1}}B(n∈{N^*},n>1)$的中点,设数列{an},{bn}满足:向量$\overrightarrow{{B_n}{A_n}}={a_n}\overrightarrow{CA}+{b_n}\overrightarrow{CB}(n∈{N^*})$,有下列四个命题,其中假命题是( )
| A. | 数列{an}是单调递增数列,数列{bn}是单调递减数列 | |
| B. | 数列{an+bn}是等比数列 | |
| C. | 数列$\{\frac{a_n}{b_n}\}$有最小值,无最大值 | |
| D. | 若△ABC中,C=90°,CA=CB,则$|\overrightarrow{{B_n}{A_n}}|$最小时,${a_n}+{b_n}=\frac{1}{2}$ |
13. 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
10.执行如图所示的程序框图,若输入x=20,则输出的y的值为( )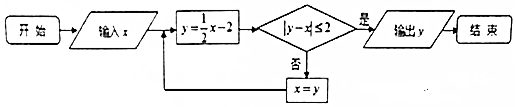

| A. | 2 | B. | -1 | C. | -$\frac{13}{4}$ | D. | -$\frac{5}{2}$ |