题目内容
7.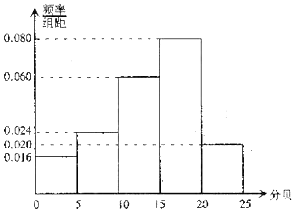 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:(Ⅰ)现从听力等级为(0,10]的同学中任意抽取出4人,记听力非常优秀的同学人数X,求X的分布列与数学期望.
(Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发声情况不同,由强到弱的次序分别为1,2,3,4,测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号a1,a2,a3,a4(其中a1,a2,a3,a4为1,2,3,4的一个排列),若Y为两次排序偏离程度的一种描述,Y=|1-a1|+|2-a2|+|3-a3|+|4-a4|,求Y≤2的概率.
分析 (Ⅰ)根据题意得X的可能值为0,1,2,3,4,
求出对应的概率,写出X的分布列,计算数学期望值;
(Ⅱ)序号a1,a2,a3,a4的排列总数为${A}_{4}^{4}$,
计算Y≤2对应的种数为Y=0或Y=2时共4种,求出对应的概率值.
解答 解:(Ⅰ)X的可能值为0,1,2,3,4,
则P(X=0)=$\frac{{C}_{6}^{4}}{{C}_{10}^{4}}$=$\frac{15}{210}$,P(X=1)=$\frac{{C}_{4}^{1}{C}_{6}^{3}}{{C}_{10}^{4}}$=$\frac{80}{210}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{6}^{2}}{{C}_{10}^{4}}$=$\frac{90}{210}$,P(X=3)=$\frac{{C}_{4}^{3}{•C}_{6}^{1}}{{C}_{10}^{4}}$=$\frac{24}{210}$,
P(X=4)=$\frac{{C}_{4}^{4}}{{C}_{10}^{4}}$=$\frac{1}{210}$;
∴X的分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{15}{210}$ | $\frac{80}{210}$ | $\frac{90}{210}$ | $\frac{24}{210}$ | $\frac{1}{210}$ |
(Ⅱ)序号a1,a2,a3,a4的排列总数为${A}_{4}^{4}$=24种,
∵Y=|1-a1|+|2-a2|+|3-a3|+|4-a4|,
当Y=0时,a1=1,a2=2,a3=3,a4=4;
当Y=|1-a1|+|2-a2|+|3-a3|+|4-a4|=2时,
a1,a2,a3,a4的可能取值为:
a1=1,a2=2,a3=4,a4=3;
a1=1,a2=3,a3=2,a4=4;
a1=2,a2=1,a3=3,a4=4;
∴Y≤2的概率为P(Y≤2)=$\frac{4}{24}$=$\frac{1}{6}$.
点评 本题主要考查了离散型随机变量的分布列与数学期望的应用问题,是综合题.

练习册系列答案
相关题目
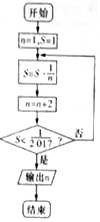
15.已知{an}是首项为1的等比数列,Sn是{an}的前n项和,且9S3=S6,则数列{anan+1}的前2017项和为( )
| A. | 22017-1 | B. | 22017-2 | C. | $\frac{1}{3}({{4^{2017}}-1})$ | D. | $\frac{2}{3}({{4^{2017}}-1})$ |
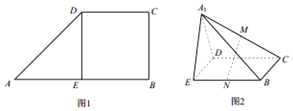 如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.
如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.