执行如图的程序框图.则输出的n为13．题目和参考答案——青夏教育精英家教网—

题目内容

18．执行如图的程序框图，则输出的n为13．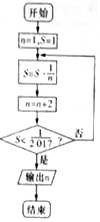

分析算法的功能是求满足S=1×$\frac{1}{3}$×$\frac{1}{5}$×…$\frac{1}{n}$＜$\frac{1}{2017}$的最大的正整数n+2的值，验证S=1•3•…•13＞2017，从而确定输出的n值．

解答解：由程序框图知：算法的功能是求满足S=1×$\frac{1}{3}$×$\frac{1}{5}$×…$\frac{1}{n}$＜$\frac{1}{2017}$的最大的正整数n+2的值，
∵S=1×3×…×13＞2017，
∴输出n=13．
故答案为：13．

点评本题考查了直到型循环结构的程序框图，关键框图的流程判断算法的功能是解答本题的关键，属于基础题．

练习册系列答案

9．设公比大于零的等比数列{a_n}的前n项和为S_n，且a₁=1，S₄=5S₂，数列{a_n}的通项公式（　　）

a_n=2^n-1

a_n=3ⁿ

a_n=5ⁿ

6．在复平面内，若z=m²（1+i）-m（4+i）-6i，求实数m的取为何值时，复数z 是：
（1）虚数
（2）对应的点在第一象限．

13．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞0，b＞0）的两个焦点为F₁、F₂，点A在双曲线第一象限的图象上，△AF₁F₂的面积为1，且sin∠A F₁F₂=$\frac{1}{\sqrt{5}}$，cos∠F₁AF₂=$\frac{4}{5}$
（1）求双曲线的方程
（2）已知直线y=kx+1与双曲线相交于不同两点，求实数k的取值范围．

3．已知函数f（x）（x∈R）的图象上任一点（x₀，y₀）处的切线方程为y-y₀=（x₀-2）（x₀²-1）（x-x₀），那么函数f（x）的单调递减区间是（　　）

10．已知集合$A=\left\{{x|lnx≤0}\right\}，B=\left\{{x∈R|x≥\frac{1}{2}}\right\}$，则A∩B=（　　）

A．

$（{-∞，-\frac{1}{2}}）∪[{\frac{1}{2}，1}]$

7．

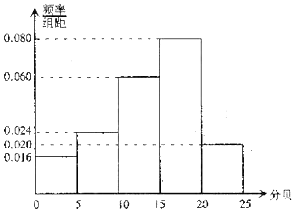人耳的听力情况可以用电子测听器检测，正常人听力的等级为0-25db（分贝），并规定测试值在区间（0，5]为非常优秀，测试值在区间（5，10]为优秀，某班50名同学都进行了听力测试，所得测试值制成频率分布直方图：
（Ⅰ）现从听力等级为（0，10]的同学中任意抽取出4人，记听力非常优秀的同学人数X，求X的分布列与数学期望．
（Ⅱ）在（Ⅰ）中抽出的4人中任选一人参加一个更高级别的听力测试，测试规则如下：四个音叉的发声情况不同，由强到弱的次序分别为1，2，3，4，测试前将音叉随机排列，被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号a₁，a₂，a₃，a₄（其中a₁，a₂，a₃，a₄为1，2，3，4的一个排列），若Y为两次排序偏离程度的一种描述，Y=|1-a₁|+|2-a₂|+|3-a₃|+|4-a₄|，求Y≤2的概率．

8．函数$f（x）={sin^2}x+\sqrt{3}sinxcosx$在区间$[{\frac{π}{4}，\frac{π}{2}}]$上的最小值为（　　）

A．

B．

$\frac{{1+\sqrt{3}}}{2}$

试题分类