题目内容
17.等比数列{an}中,a3=2,a5=6,则a9=54.分析 利用等比数列的通项公式及其性质即可得出.
解答 解:设等比数列{an}的公比为q,∵a3=2,a5=6,
∴q2=3,
则a9=${a}_{5}{q}^{4}$=6×32=54.
故答案为:54.
点评 本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
8.函数$f(x)={sin^2}x+\sqrt{3}sinxcosx$在区间$[{\frac{π}{4},\frac{π}{2}}]$上的最小值为( )
| A. | 1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $1+\sqrt{3}$ |
5.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{3x-2y-6≤0}\\{y≥1}\end{array}\right.$,则目标函数z=x+3y的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{17}{3}$ |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一条渐近线与直线x+y+1=0垂直,则该双曲线的焦距为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
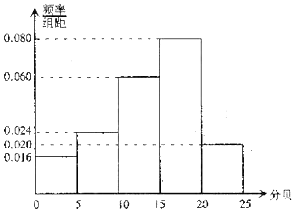 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图: