题目内容

9．已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（　　）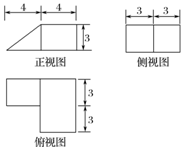
A．72 cm3B．90 cm3C．108 cm3D．138 cm3

分析 由三视图可知：该几何体由一个三棱柱与一个长方体组成的．

解答 解：由三视图可知：该几何体由一个三棱柱与一个长方体组成的．
该几何体的体积V=$\frac{1}{2}×4×3×3$+3×4×6
=90cm3．
故选：B．

点评 本题考查了三棱柱与一个长方体的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
15．已知函数f（x）=$\frac{sinx}{x}$．
（Ⅰ）求曲线y=f（x）在点A（π，f（π））处的切线方程；
（Ⅱ）证明：若x∈（0，π），则f'（x）＜0；
（Ⅲ）若0＜α＜$\frac{π}{2}$＜β＜2π，判定f（α）与f（β）的大小关系，并证明你的结论．
20．已知函数f（x）=$\frac{1+alnx}{x}$（a∈R）．
（1）当a=1时，求函数f（x）的极值；
（2）讨论函数f（x）的单调性；
（3）证明：ln（$\frac{1}{{2}^{2}}$+1）+ln（$\frac{1}{{3}^{2}}$+1）+…+ln（$\frac{1}{{n}^{2}}$+1）＜1（n≥2，n∈N*）
17．设变量x，y满足约束条件$\left\{\begin{array}{l}{3x+y-6≥0}\\{x-y-2≤0}\\{y≤a}\end{array}$，且目标函数z=y-2x的最小值为-7，则实数a等于3．
4．已知$\overrightarrow a$=（2，1），
（1）如果|$\overrightarrow b$|=$2\sqrt{5}$，且向量$\overrightarrow a$与$\overrightarrow b$共线，求$\overrightarrow b$的坐标表示；
（2）如果|$\overrightarrow b$|=$2\sqrt{10}$，且向量$\overrightarrow a$与$\overrightarrow b$夹角为$\frac{3π}{4}$，求$\overrightarrow b$的坐标表示．
14．命题：①半径为2，圆心角的弧度数为$\frac{1}{2}$的扇形的周长为5；
②若α、β为第三象限角，且α＞β，则cosα＞cosβ；
③若直线的斜率是-cosθ，则其倾斜角的取值范围是[$\frac{π}{4}，\frac{π}{2}}）∪（{\frac{π}{2}，\frac{3π}{4}}$]；
④当x≠$\frac{kπ}{2}$（k∈Z））时，$\frac{sinx+tanx}{cosx+cotx}$的值恒正．其中正确的命题是①④．
1．在等差数列{an}中，已知a1+a6=12，a4=7
（1）求a9；
（2）求{an}前n项和Sn．
18．下列函数中，最小值是2的是（　　）
A．y=x+$\frac{1}{x}$B．y=sinx+$\frac{1}{sinx}$（0$＜x＜\frac{π}{2}$）
C．y=lgx+$\frac{1}{lgx}$（1＜x＜10）D．y=x+$\frac{2}{\sqrt{x}}$-1
19．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，以F1为圆心，|F1F2|为半径的圆与双曲线在第一、二象限内依次交于A，B两点，若|F1B|=3|F2A|，则该双曲线的离心率为（　　）
A．$\frac{5}{4}$B．$\frac{4}{3}$C．$\frac{3}{2}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网