题目内容
15.已知函数f(x)=$\frac{sinx}{x}$.(Ⅰ)求曲线y=f(x)在点A(π,f(π))处的切线方程;
(Ⅱ)证明:若x∈(0,π),则f'(x)<0;
(Ⅲ)若0<α<$\frac{π}{2}$<β<2π,判定f(α)与f(β)的大小关系,并证明你的结论.
分析 (Ⅰ)求出原函数的导函数,得到f′(π),再求出f(π),代入直线方程的点斜式得答案;
(Ⅱ)求出原函数的导函数f′(x)=$\frac{x•cosx-sinx}{{x}^{2}}$,令g(x)=x•cosx-sinx,可得g′(x)<0,得到g(x)在(0,π)上为减函数,又g(x)<g(0)=0.可得f′(x)<0;
(Ⅲ)由(Ⅱ)可知,f(x)在(0,π)上为减函数,得到0<α<$\frac{π}{2}$<β<π时,f(α)>f(β);当π≤β<2π时,f(β)=$\frac{sinβ}{β}$<0,可得f(α)>f(β).
解答 解:(Ⅰ)f′(x)=$\frac{x•cosx-sinx}{{x}^{2}}$,
f′(π)=-$\frac{1}{π}$,而f(π)=0,
∴曲线y=f(x)在点A(π,f(π))处的切线方程为y-0=$-\frac{1}{π}$(x-π),
即x+πy-π=0;
证明:(Ⅱ)f′(x)=$\frac{x•cosx-sinx}{{x}^{2}}$,
令g(x)=x•cosx-sinx,则g′(x)=cosx-x•sinx-cosx=-xsinx<0,
∴g(x)在(0,π)上为减函数,则g(x)<g(0)=0.
∴f′(x)<0;
解:(Ⅲ)若0<α<$\frac{π}{2}$<β<2π,则f(α)>f(β).
事实上,当0<α<$\frac{π}{2}$<β<π时,
由(Ⅱ)知f′(x)<0,
故f(x)在(0,π)上为减函数,
由0<α<$\frac{π}{2}$<β<π,可得f(α)>f(β);
当0<α<$\frac{π}{2}$,π≤β<2π时,f(α)=$\frac{sinα}{α}>0$,f(β)=$\frac{sinβ}{β}$<0,可得f(α)>f(β).
综上,若0<α<$\frac{π}{2}$<β<2π,则f(α)>f(β).
点评 本题考查利用导数研究函数的单调性,考查利用导数求过曲线上某点处的切线方程,体现了分类讨论的数学思想方法,是中档题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案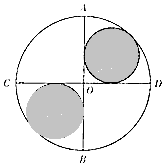 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
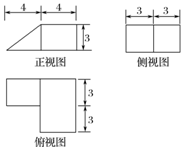
| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
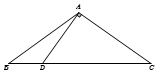 如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3. 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.