题目内容
18.下列函数中,最小值是2的是( )| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$(0$<x<\frac{π}{2}$) | ||
| C. | y=lgx+$\frac{1}{lgx}$(1<x<10) | D. | y=x+$\frac{2}{\sqrt{x}}$-1 |
分析 利用函数的单调性或基本不等式求解函数的最小值,推出结论.
解答 解:y=x+$\frac{1}{x}$,x>0时,函数的最小值为2.x<0时,y≤-2,所以函数的最小值不是2,A不正确;
y=sinx+$\frac{1}{sinx}$(0$<x<\frac{π}{2}$)可得x=$\frac{π}{2}$时,函数取得最小值,所以B不正确;
y=lgx+$\frac{1}{lgx}$(1<x<10)当x=10时函数的最小值为2,所以C不正确;
y=x+$\frac{2}{\sqrt{x}}$-1,函数的定义域为x>0,y=x+$\frac{1}{\sqrt{x}}$+$\frac{1}{\sqrt{x}}$-1≥3$\root{3}{x•\frac{1}{\sqrt{x}}•\frac{1}{\sqrt{x}}}$-1=2,当且仅当x=1时取等号.所以D正确;
故选:D.
点评 本题考查函数的最值的求法,基本不等式的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
9.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
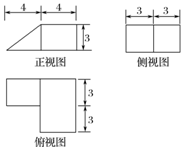

| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
6.如图是某几何体的三视图,图中小方格单位长度为1,则该几何体外接球的表面积为( )

| A. | 8π | B. | 12π | C. | 16π | D. | 24π |
13.在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,P是三角形BDC'内的动点,EP⊥BC',则P的轨迹长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
8.已知函数f(x)的部分图象如图,则f(x)的解析式可能为( )


| A. | f(x)=xsinx | B. | f(x)=xcosx-sinx | C. | f(x)=xcosx | D. | f(x)=xcosx+sinx |