题目内容
17.设变量x,y满足约束条件$\left\{\begin{array}{l}{3x+y-6≥0}\\{x-y-2≤0}\\{y≤a}\end{array}$,且目标函数z=y-2x的最小值为-7,则实数a等于3.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,结合数形结合即可得到结论.
解答 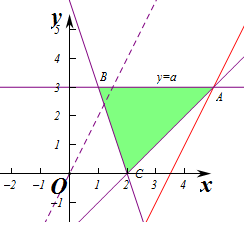 解:由z=y-2x,则y=2x+z
解:由z=y-2x,则y=2x+z
作出不等式组对应的平面区域如图:
平移直线y=2x+z,由图象知当直线y=2x+z,经过点A时,直线y=2x+z的截距最小,此时z最小,
即此时z=y-2x=-7,
由$\left\{\begin{array}{l}{y-2x=-7}\\{x-y-2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$,即A(5,3),
此时A也在y=a上,∴a=3,
故答案为:3.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
5.设$\frac{1}{2}$<($\frac{1}{2}$)b<($\frac{1}{2}$)a,则下列不等关系成立的是( )
| A. | aa<ab<ba | B. | aa<ba<ab | C. | ab<aa<ba | D. | ab<ba<aa |
12.若$cosα=-\frac{3}{5}$,且$α∈[{\frac{π}{2},π}]$,则$cos({α-\frac{π}{4}})$=( )
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
9.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
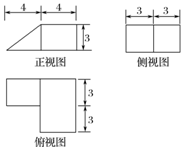

| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
6.如图是某几何体的三视图,图中小方格单位长度为1,则该几何体外接球的表面积为( )

| A. | 8π | B. | 12π | C. | 16π | D. | 24π |