题目内容
20.已知函数f(x)=$\frac{1+alnx}{x}$(a∈R).(1)当a=1时,求函数f(x)的极值;
(2)讨论函数f(x)的单调性;
(3)证明:ln($\frac{1}{{2}^{2}}$+1)+ln($\frac{1}{{3}^{2}}$+1)+…+ln($\frac{1}{{n}^{2}}$+1)<1(n≥2,n∈N*)
分析 (1)a=1时,f(x)=$\frac{1+lnx}{x}$(x>0),f′(x)=$\frac{-lnx}{{x}^{2}}$,可知:x=1时,函数f(x)取得极大值,
(2)f′(x)=$\frac{\frac{a}{x}•x-(1+alnx)}{{x}^{2}}$=$\frac{-alnx+a-1}{{x}^{2}}$.(x>0).对a分类讨论,利用导数研究其单调性即可得出.
(3)下面证明:x>1时,lnx<x-1.令g(x)=lnx-x+1,g(1=0.由g′(x)=$\frac{1}{x}$-1<0,可得函数g(x)在(1,+∞)上单调递减,可得lnx<x-1.因此ln($\frac{1}{{n}^{2}}$+1)<$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$(n≥2).利用裂项求和与数列的单调性即可得出证明.
解答 (1)解:a=1时,f(x)=$\frac{1+lnx}{x}$(x>0),f′(x)=$\frac{\frac{1}{x}•x-(1+lnx)}{{x}^{2}}$=$\frac{-lnx}{{x}^{2}}$,可知:x=1时,函数f(x)取得极大值,
f(1)=1.
(2)解:f′(x)=$\frac{\frac{a}{x}•x-(1+alnx)}{{x}^{2}}$=$\frac{-alnx+a-1}{{x}^{2}}$.(x>0).
a=0时,f′(x)=$\frac{-1}{x}$<0,因此函数f(x)在(0,+∞)上单调递减.
a≠0时,f′(x)=$\frac{-a(lnx-\frac{a-1}{a})}{{x}^{2}}$(x>0).令f′(x)=0,解得x=${e}^{\frac{a-1}{a}}$.
a<0时,函数f(x)在$(0,{e}^{\frac{a-1}{a}})$上单调递减;在$({e}^{\frac{a-1}{a}},+∞)$上单调递增.
0<a时,函数f(x)在$(0,{e}^{\frac{a-1}{a}})$上单调递增;在$({e}^{\frac{a-1}{a}},+∞)$上单调递减.
(3)证明:下面证明:x>1时,lnx<x-1.
令g(x)=lnx-x+1,g(1=0.
g′(x)=$\frac{1}{x}$-1<0,∴函数g(x)在(1,+∞)上单调递减,
∴g(x)<g(1)=0.
∴lnx<x-1.
∴ln($\frac{1}{{n}^{2}}$+1)<$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$(n≥2).
∴ln($\frac{1}{{2}^{2}}$+1)+ln($\frac{1}{{3}^{2}}$+1)+…+ln($\frac{1}{{n}^{2}}$+1)<$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})$=1-$\frac{1}{n}$<1(n≥2,n∈N*).
点评 本题考查了利用导数研究函数的单调性极值与最值、分类讨论、方程与不等式的解法、裂项求和方法、放缩法,考查了推理能力与计算能力,属于难题.

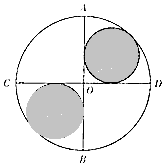 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
| A. | aa<ab<ba | B. | aa<ba<ab | C. | ab<aa<ba | D. | ab<ba<aa |
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
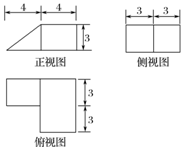
| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.