题目内容
19.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,以F1为圆心,|F1F2|为半径的圆与双曲线在第一、二象限内依次交于A,B两点,若|F1B|=3|F2A|,则该双曲线的离心率为( )| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 由题意可知2|F2A|=2a,即|F2A|=a,|F1A|=丨F1F2丨=2c,则2c=3a,利用椭双曲线的离心率公式,即可求得该双曲线的离心率
解答  解:根据已知可得,|F1B|=|F1A|=3|F2A|,又|F1A|-|F2A|=2a,
解:根据已知可得,|F1B|=|F1A|=3|F2A|,又|F1A|-|F2A|=2a,
∴2|F2A|=2a,即|F2A|=a,
又因为|F1A|=丨F1F2丨=2c,则2c=3a,
∴e=$\frac{c}{a}$=$\frac{3}{2}$,
故选:C.
点评 本题考查双曲线的简单几何性质,考查双曲线的定义,数形结合思想,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
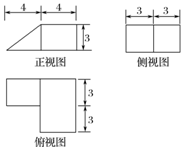

| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
14.已知集合下列角中,终边在y轴非正半轴上的是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
4.已知集合A={x|y=lg(4-3x-x2)},集合B={x|2x<1},则A∩B=( )
| A. | {x|x<0} | B. | {x|-4<x<0} | C. | {x|-4<x<1} | D. | {x|x<1} |
8.已知函数f(x)的部分图象如图,则f(x)的解析式可能为( )


| A. | f(x)=xsinx | B. | f(x)=xcosx-sinx | C. | f(x)=xcosx | D. | f(x)=xcosx+sinx |
9.已知一几何体的三视图如图所示,则该几何体的体积为( )
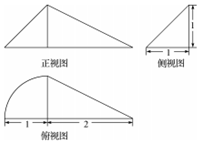

| A. | $\frac{π}{6}+\frac{1}{3}$ | B. | $\frac{π}{12}+1$ | C. | $\frac{π}{12}+\frac{1}{3}$ | D. | $\frac{π}{4}+\frac{1}{3}$ |