题目内容
4.已知$\overrightarrow a$=(2,1),(1)如果|$\overrightarrow b$|=$2\sqrt{5}$,且向量$\overrightarrow a$与$\overrightarrow b$共线,求$\overrightarrow b$的坐标表示;
(2)如果|$\overrightarrow b$|=$2\sqrt{10}$,且向量$\overrightarrow a$与$\overrightarrow b$夹角为$\frac{3π}{4}$,求$\overrightarrow b$的坐标表示.
分析 (1)设$\overrightarrow{b}=(x,y)$,由向量的模及斜率共线列关于x,y的方程组求解;
(2)设$\overrightarrow{b}=(x,y)$,由向量的模及斜率夹角列关于x,y的方程组求解.
解答 解:(1)设$\overrightarrow{b}=(x,y)$,由|$\overrightarrow b$|=$2\sqrt{5}$,且向量$\overrightarrow a$与$\overrightarrow b$共线,
得$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=20}\\{2y-x=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
∴$\overrightarrow b=(4,2)$或$\overrightarrow b=(-4,-2)$;
(2)设$\overrightarrow{b}=(x,y)$,由|$\overrightarrow b$|=$2\sqrt{10}$,且向量$\overrightarrow a$与$\overrightarrow b$夹角为$\frac{3π}{4}$,
得$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=40}\\{\frac{2x+y}{\sqrt{5}•\sqrt{{x}^{2}+{y}^{2}}}=-\frac{\sqrt{2}}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-6}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-6}\end{array}\right.$.
∴$\overrightarrow b=(-6,2)$或$\overrightarrow b=(-2,-6)$.
点评 本题考查平面向量的数量积运算,考查向量共线及垂直的坐标运算,考查向量模的求法,是中档题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
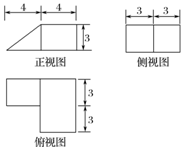
| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
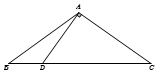 如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3. 某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为162πml,设圆柱的高度为hcm,底面半径为rcm,且h≥6r.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数,且0<3m<n).
某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为162πml,设圆柱的高度为hcm,底面半径为rcm,且h≥6r.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数,且0<3m<n).