题目内容
19.已知3i-2是关于x的方程2x2+px+q=0的一个根,则实数p+q=34.分析 3i-2是关于x的方程2x2+px+q=0的一个根,则-3i-2也是关于x的方程2x2+px+q=0的一个根,再利用根与系数的关系即可得出.
解答 解:∵3i-2是关于x的方程2x2+px+q=0的一个根,∴-3i-2也是关于x的方程2x2+px+q=0的一个根,
∴3i-2+(-3i-2)=-$\frac{p}{2}$,(3i-2)(-3i-2)=$\frac{q}{2}$,
解得p=8,q=26.
∴p+q=34.
故答案为:34.
点评 本题考查了实系数一元二次方程的虚根成对原理、根与系数的关系、复数的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.设复数z=$\frac{1}{1-i}$+i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 2 |
14.如果a>b>0,那么下列不等式中不正确的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ab>b2 | D. | a2>ab |
4.复数z=$\frac{a-i}{1+i}$(a∈R,i是虚数单位)在复平面上对应的点不可能位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.定义在区间(0,+∞)上的函数f(x)>0,且f(x)<xf′(x)<2f(x)恒成立,其中f′(x)为f(x)的导函数,则( )
| A. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | B. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ | C. | $\frac{1}{2}$<$\frac{f(1)}{f(2)}$<1 | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
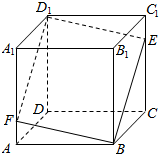 如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中真命题的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中真命题的个数是( )