题目内容
若F1、F2是双曲线
-
=1的两个焦点,点P是该双曲线上一点,满足|PF1|+|PF2|=9,则|PF1|•|PF2|=( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、4 | ||
| B、5 | ||
C、
| ||
| D、2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:不妨设P是双曲线右支上一点,则|PF1|-|PF2|=4,由|PF1|+|PF2|=9,求出|PF1|=
,|PF2|=
,即可求出|PF1|•|PF2|的值.
| 13 |
| 2 |
| 5 |
| 2 |
解答:
解:不妨设P是双曲线右支上一点,则|PF1|-|PF2|=4,
∵|PF1|+|PF2|=9,
∴|PF1|=
,|PF2|=
,
∴|PF1|•|PF2|=
.
故选:C.
∵|PF1|+|PF2|=9,
∴|PF1|=
| 13 |
| 2 |
| 5 |
| 2 |
∴|PF1|•|PF2|=
| 65 |
| 4 |
故选:C.
点评:本题考查双曲线的方程,考查双曲线的定义,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
一简单组合体的三视图如图所示,则该组合体的体积为( )


| A、16-π | B、12-4π |
| C、12-2π | D、12-π |
设a=log210,b=log315,c=log735,则( )
| A、c>a>b |
| B、b>c>a |
| C、b>a>c |
| D、a>b>c |
若实数x,y满足
,则实数m=
的取值范围是( )
|
| y-1 |
| x+1 |
| A、(-1,1) | ||||
| B、[-1,1) | ||||
C、(-
| ||||
D、[-
|
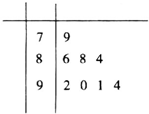 某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是
某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是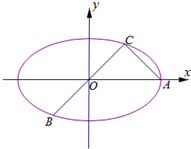 如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且