Question

5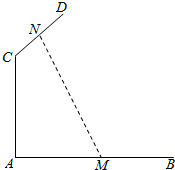．如图，AB、CD为互相垂直的两异面直线，AC⊥AB，AC⊥CD，线段AC长为2，M∈AB，N∈CD，P为MN中点，且线段MN长为4，则点P的轨迹所形成的面积为（　　）

• A． 0
• B． 3π
• C． 16π
• D． 8π

Answer 1

分析 作AD′∥CD，NN′⊥AD′，P′为N′M的中点，则PP′⊥平面ABD′，且PP′=1，P′的轨迹与P的轨迹一样，由已知得H到A点距离一直是$\sqrt{3}$，从而得到P点的轨迹是线A点的圆．

解答 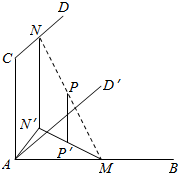解：作AD′∥CD，NN′⊥AD′，P′为N′M的中点，
∴PP′⊥平面ABD′，且PP′=1，
∴P′的轨迹与P的轨迹一样，
N′M²=NM²-NN^'2，解得N′M=2$\sqrt{3}$，
如图一，P′始终是HA的中点，
N′H²+MH²=AN^'2+AM²=N′M²=12，
即H到A点距离一直是$\sqrt{3}$，
∴P′点的轨迹即P点轨迹是线A点的圆，面积为3π．
故选：B．

点评 本题考查点的轨迹所形成面积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．