题目内容
8．椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1的离心率为$\frac{3}{4}$．分析 根据题意，由椭圆的标准方程可得a=4，b=$\sqrt{7}$，进而可得c的值，由离心率计算公式e=$\frac{c}{a}$计算可得答案．
解答 解：根据题意，椭圆的标准方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1，
则其中a=4，b=$\sqrt{7}$，
则c=$\sqrt{16-7}$=3，
故其离心率e=$\frac{c}{a}$=$\frac{3}{4}$；
故答案为：$\frac{3}{4}$．
点评 本题考查椭圆的性质，涉及椭圆离心率的计算，关键是牢记椭圆离心率的公式．
练习册系列答案
阅读快车系列答案
相关题目
18．已知锐角α，β满足$\frac{sinα}{cosβ}$+$\frac{sinβ}{cosα}$＜2，设f（x）=logax（0＜a＜1），则下列判断正确的是（ ）
| A． | f（sinα）＞f（cosβ） | B． | f（cosα）＞f（sinβ） | C． | f（sinα）＜f（sinβ） | D． | f（cosα）＜f（cosβ） |
16．圆x2+（y-5）2=25的圆心到直线3x+4y-5=0的距离等于（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
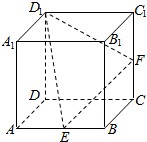如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别是AB，CC1的中点，过点E，F1D1的截面与正方体的下底面相交于直线l，