题目内容
求由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积.
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:利用定积分的几何意义表示区域面积,即可得出结论.
解答:
解:由题意,由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形如图:
面积为
[-x(x-1)]dx=-(
x3-
x2)|
=
.

面积为
| ∫ | 1 0 |
| 1 |
| 3 |
| 1 |
| 2 |
1 0 |
| 1 |
| 6 |
点评:本小题考查根据定积分的几何意义,以及会利用定积分求图形面积的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
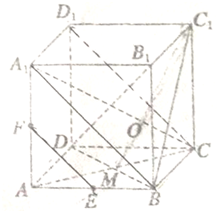 如图,在正方体ABCD-A1B1C1D1,对角线A1C与平面BDC1交于点O.AC、BD交于点M、E为AB的中点,F为AA1的中点,
如图,在正方体ABCD-A1B1C1D1,对角线A1C与平面BDC1交于点O.AC、BD交于点M、E为AB的中点,F为AA1的中点,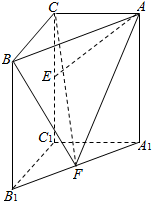 如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.