题目内容
2.已知θ∈($\frac{π}{2}$,π),tan(θ-$\frac{π}{4}$)=-$\frac{4}{3}$,则sin(θ+$\frac{π}{4}$)=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
分析 由已知及两角差的正切函数公式可求tanθ=$\frac{sinθ}{cosθ}$=-$\frac{1}{7}$,利用同角三角函数基本关系式可求sinθ,cosθ的值,进而利用两角和的正弦函数公式即可计算得解.
解答 解:∵θ∈($\frac{π}{2}$,π),可得:cosθ<0,sinθ>0,
∵tan(θ-$\frac{π}{4}$)=-$\frac{4}{3}$,
∴$\frac{tanθ-1}{1+tanθ}$=-$\frac{4}{3}$,
∴解得:tanθ=$\frac{sinθ}{cosθ}$=-$\frac{1}{7}$,①
又∵sin2θ+cos2θ=1,②
∴联立①②解得:sinθ=$\frac{\sqrt{2}}{10}$,cosθ=-$\frac{7\sqrt{2}}{10}$,
∴sin(θ+$\frac{π}{4}$)=sinθcos$\frac{π}{4}$+cosθsin$\frac{π}{4}$
=$\frac{\sqrt{2}}{2}$($\frac{\sqrt{2}}{10}$-$\frac{7\sqrt{2}}{10}$)=-$\frac{3}{5}$.
故选:D.
点评 本题主要考查了两角差的正切函数公式,同角三角函数基本关系式,两角和的正弦函数公式在三角函数化简求值中的综合应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.若将函数y=2cos(2x-$\frac{π}{3}$)的图象向右平移$\frac{1}{4}$个周期后,所得图象对应的函数为( )
| A. | $y=2sin(2x-\frac{π}{4})$ | B. | $y=2sin(2x-\frac{π}{3})$ | C. | $y=2sin(2x+\frac{π}{4})$ | D. | $y=2sin(2x+\frac{π}{3})$ |
11.已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2,下列命题为真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
12.阅读如图的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为( )
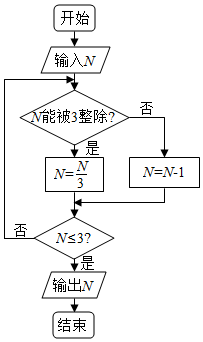

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
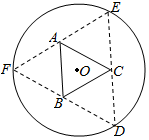 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.
如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.