题目内容
7.若将函数y=2cos(2x-$\frac{π}{3}$)的图象向右平移$\frac{1}{4}$个周期后,所得图象对应的函数为( )| A. | $y=2sin(2x-\frac{π}{4})$ | B. | $y=2sin(2x-\frac{π}{3})$ | C. | $y=2sin(2x+\frac{π}{4})$ | D. | $y=2sin(2x+\frac{π}{3})$ |
分析 利用三角函数的图象变换,化简函数的解析式即可得到选项.
解答 解:将函数y=2cos(2x-$\frac{π}{3}$)的图象向右平移$\frac{1}{4}$个周期后,可得函数y=2cos(2x-$\frac{π}{2}$-$\frac{π}{3}$)=2cos[$\frac{π}{2}$-(2x-$\frac{π}{3}$)]=2sin(2x-$\frac{π}{3}$)的图象.
故选:B.
点评 本题考查三角函数的图象变换,三角函数的化简求解,考查计算能力.

练习册系列答案
相关题目
13.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080,则下列各数中与$\frac{M}{N}$最接近的是( )
(参考数据:lg3≈0.48)
(参考数据:lg3≈0.48)
| A. | 1033 | B. | 1053 | C. | 1073 | D. | 1093 |
2.已知θ∈($\frac{π}{2}$,π),tan(θ-$\frac{π}{4}$)=-$\frac{4}{3}$,则sin(θ+$\frac{π}{4}$)=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
12.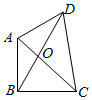 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )| A. | I1<I2<I3 | B. | I1<I3<I2 | C. | I3<I1<I2 | D. | I2<I1<I3 |
16.从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是( )
| A. | $\frac{5}{18}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |