题目内容
函数f(x)=
的定义域是( )
| 1 |
| log3(x-2) |
| A、(-∞,2) |
| B、(2,+∞) |
| C、(2,3)∪(3,+∞) |
| D、(2,5)∪(5,+∞) |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件即可求函数的定义域.
解答:
解:要使函数有意义,则
,
即
,
解得x>2且x≠3,
故函数的定义域为(2,3)∪(3,+∞),
故选:C
|
即
|
解得x>2且x≠3,
故函数的定义域为(2,3)∪(3,+∞),
故选:C
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中,与函数y=x相同的函数是( )
A、y=
| ||||
B、y=(
| ||||
| C、y=lg10x | ||||
| D、y=2log2x |
已知向量
=(1,-2),
=(-
,y),若
∥
,则y=( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
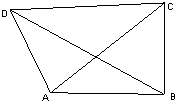 如图:在平面四边形ABCD中,AB=3
如图:在平面四边形ABCD中,AB=3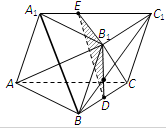 如图,在三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.