题目内容
6.某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如表:| 使用智能手机人数 | 不使用智能手机人数 | 合计 | |
| 学习成绩优秀人数 | 4 | 8 | 12 |
| 学习成绩不优秀人数 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为A组,不使用智能手机且成绩优秀的8位同学记为B组,计划从A组推选的2人和B组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自A、B两组的概率.
分析 (I)根据所给的数据做出这组数据的观测值,把观测值同临界值进行比较,得到该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响.
(II)本题是一个等可能事件的概率,试验发生包含的事件数是10种结果,满足条件的事件是挑选的两人恰好分别来自A、B两组,可以通过列举得到结果.
解答 解:(I)根据卡方公式求得K2=$\frac{30(8-128)^{2}}{20×10×12×18}$=10,
因为7.897<K2<10.828
所以该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响. …4 分
(II)记A组推选的两名同学为a1,a2,B组推选的三名同学为b1,b2,b3,
则从中随机选出两名同学包含如下10个基本事件:(a1,a2),(a1,b1),
(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3)…7 分
记挑选的两人恰好分别来自A、B两组为事件Z,
则事件Z包含如下6 个基本事件:(a1,b1),(a1,b2),(a1,b3),(a2,b1),
(a2,b2),(a2,b3)…9 分
故$P(Z)=\frac{6}{10}=\frac{3}{5}$.
即挑选的两人恰好分别来自A、B两组的概率是$\frac{3}{5}$.…12 分
点评 本题考查独立性检验的应用和等可能事件的概率,本题解题的关键是正确理解观测值对应的概率的意义.

练习册系列答案
相关题目
12.“x>0”是“(x-2)(x-4)<0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.A、F分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左顶点和右焦点,A、F在双曲线的一条渐近线上的射影分别为B、Q,O为坐标原点,△ABO与△FQO的面积之比为$\frac{1}{2}$,则该双曲线的离心率为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
11.在Rt△ABC中,∠B=60°过直角顶点A在∠BAC内随机作射线AD,交斜边BC于点D,则BD>BA的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
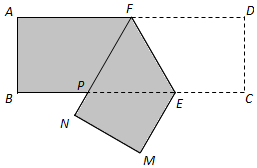 如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.
如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.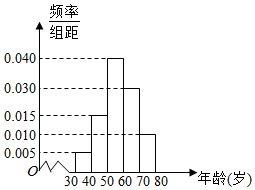 某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.
某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.