题目内容
16.实数x,y满足$\left\{\begin{array}{l}{y-2x≤-2}\\{y≥1}\\{x+y≤4}\end{array}\right.$,则$\frac{y}{x}$的取值范围是$[\frac{1}{3},1]$.分析 作出不等式组对应的平面区域,设k=$\frac{y}{x}$,利用目标函数的几何意义,求k的最值即可.
解答 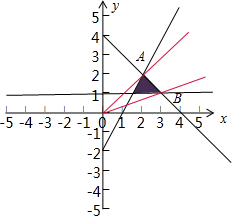 解:设k=$\frac{y}{x}$,则k的几何意义为过原点的直线的斜率:
解:设k=$\frac{y}{x}$,则k的几何意义为过原点的直线的斜率:
作出不等式组$\left\{\begin{array}{l}{y-2x≤-2}\\{y≥1}\\{x+y≤4}\end{array}\right.$对应的平面区域如图(阴影部分ABC):
则由图象可知,过原点的直线y=kx,当直线y=kx,经过点A时,直线的斜率k最小,
当经过点A时,直线的斜率k最大,
由$\left\{\begin{array}{l}{y-2x=-2}\\{x+y=4}\end{array}\right.$,解得A(2,2),此时k=$\frac{2}{2}$=1.
由$\left\{\begin{array}{l}{y=1}\\{x+y=4}\end{array}\right.$,解得B(3,1),此时k=$\frac{1}{3}$,
∴直线y=kx的斜率k的取值范围是$\frac{1}{3}$≤k≤1,
故答案为:$[\frac{1}{3},1]$.
点评 本题主要考查线性规划的应用,根据目标函数的几何意义为过原点直线的斜率,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
相关题目
6.某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如表:
参考数据:
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为A组,不使用智能手机且成绩优秀的8位同学记为B组,计划从A组推选的2人和B组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自A、B两组的概率.
| 使用智能手机人数 | 不使用智能手机人数 | 合计 | |
| 学习成绩优秀人数 | 4 | 8 | 12 |
| 学习成绩不优秀人数 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为A组,不使用智能手机且成绩优秀的8位同学记为B组,计划从A组推选的2人和B组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自A、B两组的概率.
7.若${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中所有项系数的绝对值之和为1024,则该展开式中的常数项是( )
| A. | -270 | B. | 270 | C. | -90 | D. | 90 |
8.对于函数f(x)=atanx+bx3+cx(a、b、c∈R),选取a、b、c的一组值计算f(1)、f(-1),所得出的正确结果可能是( )
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
6.若复数z 满足z(1+i)=-2i(i为虚数单位),则复数z 在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
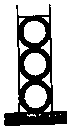 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.