题目内容

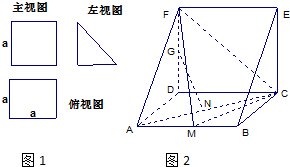
如图：△ABC中，D是AB上一点，且AB=3AD，∠B=75°，∠CDB=60°，求证：△ABC∽△CBD．
考点：相似三角形的判定
专题：解三角形
分析：设AB等于c，在△BCD中，利用正弦定理求出BC=
6
3
c，从而得到
AB
BC
=
BC
BD
，由此能证明△ABC∽△CBD．
解答： 解：设AB等于c，∵AB=3AD，∴BD=
2
3
c，
在△BCD中，
∵∠B=75°，∠CDB=60°，∴∠BCD=45°，
∴
BC
sin60°
=
BD
sin45°
，
∴BC=
BD•sin60°
sin45°
=
2
3
c•
3
2
2
2
=
6
3
c，
∴
AB
BC
=
c
6
3
c
=
6
2
，
BC
BD
=
6
3
c
2
3
c
=
6
2
，
∴
AB
BC
=
BC
BD
，又∵∠B=∠B，
∴△ABC∽△CBD．
点评：本题考查三角形相似的证明，是中档题，解题时要认真审题，注意正弦定理的合理运用．
练习册系列答案
相关题目
若关于x，y的方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线，则方程（x+cosα）2+（y+sinα）2=1所表示的圆的圆心在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
观察下列各式：
3
（1+
1
3
）＞
5
，
5
（1+
1
5
）＞
7
，
7
（1+
1
7
）＞
9
，
9
（1+
1
9
）＞
11
　…
请你根据上述特点，提炼出一个一般性命题，并用分析法加以证明．
设数列{an}的前n项和为Sn，a1=b且an=2an-1+
1
2n
（n＞1，n∈N*）
（Ⅰ）若b=-
1
8
，求a2，a3，a4；
（Ⅱ）若{an}是递增数列，求实数b的取值范围；
（Ⅲ）若?n∈N*，Sn≥S2恒成立，求实数b的取值范围．
已知以原点为中心，F（
3
，0）为右焦点的椭圆C，过点F垂直于x轴的弦AB长为4．
（1）求椭圆C的标准方程．
（2）设M、N为椭圆C上的两动点，且
OM
⊥
ON
，点P为椭圆C的右准线与x轴的交点，求
PM
•
PN
取值范围．
已知|
a
|=2，|
b
|=3
（1）若
a
，
b
两向量所成角θ=
2π
3
，求
a
•
b
．
（2）若
a
，
b
两向量所成的角θ=
π
3
，求|
a
+2
b
|的大小．
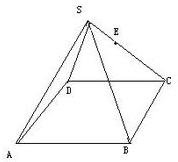在底面是菱形的四棱锥S-ABCD中，SA=SC=2a，SB=SD=
2
a，E是SC上的一点且SE=λa（0＜λ≤a），求证：对任意λ∈（0，a]，都有BD⊥AE．
（理科）设a∈R，解关于x的不等式ax2-（2a+1）x+2＞0．
一个棱柱的直观图（图2）和三视图（图1）（主视图和俯视图是正方形，左视图是等腰直角三角形）如图所示2，其中M、N分别是AB、AC的中点，G是DF上的一动点．

（1）求证：GN⊥AC
（2）当FG=GD时，证明AG∥平面FMC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网