题目内容
一个棱柱的直观图（图2）和三视图（图1）（主视图和俯视图是正方形，左视图是等腰直角三角形）如图所示2，其中M、N分别是AB、AC的中点，G是DF上的一动点．
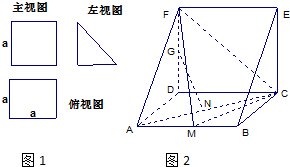
（1）求证：GN⊥AC
（2）当FG=GD时，证明AG∥平面FMC．
（1）求证：GN⊥AC
（2）当FG=GD时，证明AG∥平面FMC．
考点：直线与平面平行的判定,简单空间图形的三视图,直线与平面垂直的性质
专题：证明题,空间位置关系与距离
分析：（1）根据三视图与直观图的关系，判定面ABCD，CDFE是边长为a的正方形，再应用线面垂直的判定和性质即可证明；
（2）连结DE交FC于Q，连结QG，由中位线定理得到线线平行，再由线面平行的判定定理即可证明．
（2）连结DE交FC于Q，连结QG，由中位线定理得到线线平行，再由线面平行的判定定理即可证明．
解答：
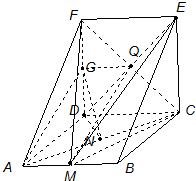（1）证明：由三视图可知面ABCD，CDFE是边长为a的正方形．
∵FD⊥CD，FD⊥AD，
∴FD⊥面ABCD，FD⊥AC，
连结DN，N是AC的中点，
∴AC⊥DN，∴AC⊥面GND，GN?面GND，
∴GN⊥AC；
（2）证明：连结DE交FC于Q，连结QG
∵G，Q，M分别是FD，FC，AB的中点，
∴GQ∥
CD，AM∥
CD，
∴AM∥GQ，AMGQ是平行四边形
∴AG∥QM，
∵AG?面FMC，MQ?面FMC，
∴AG∥平面FMC．
（1）证明：由三视图可知面ABCD，CDFE是边长为a的正方形．∵FD⊥CD，FD⊥AD，
∴FD⊥面ABCD，FD⊥AC，
连结DN，N是AC的中点，
∴AC⊥DN，∴AC⊥面GND，GN?面GND，
∴GN⊥AC；
（2）证明：连结DE交FC于Q，连结QG
∵G，Q，M分别是FD，FC，AB的中点，
∴GQ∥
| 1 |
| 2 |
| 1 |
| 2 |
∴AM∥GQ，AMGQ是平行四边形
∴AG∥QM，
∵AG?面FMC，MQ?面FMC，
∴AG∥平面FMC．
点评：本题主要考查空间直线与平面的位置关系，考查线面平行与垂直的判定和性质，同时考查三视图与直观图的关系，是一道基础题．
练习册系列答案
相关题目
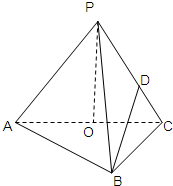如图，在三棱锥P-ABC，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠ABC=∠ADC=90゜，∠BAD=120゜，AD=AB=a，若PA=λa（λ＞0）．